Exam 9: Vectors and the Geometry of Space
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Find the set of intersection of the surfaces whose equations in spherical coordinates are and .
(Essay)
4.8/5  (41)
(41)
Find the volume of the parallelepiped below given P = (1, -3, 2), Q = (3, -1, 3), R = (2, 1, -4), and S = (-1, 2, 1). 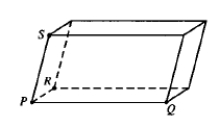
(Short Answer)
4.8/5  (44)
(44)
The planes P1: x + 2y + 3z = 2 and P2: -2x + 3y + 2z = -4 both contain the point P (2, 0, 0).Find a vector equation r = OP0 + td for the line of intersection of these planes.
(Essay)
4.9/5  (35)
(35)
Find parametric equations and symmetric equations of the line passing through the points A and B shown below. 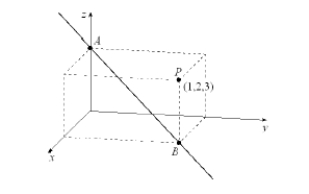
(Essay)
4.8/5  (35)
(35)
Determine whether the points A , B , and C lie on a straight line.
(Short Answer)
4.8/5  (35)
(35)
Are the planes 3x - y + 5z = 13 and x + 7y - 2z = 4 perpendicular to each other?
(Short Answer)
4.8/5  (34)
(34)
Let f(x, y) = (a) Evaluate .(b) Find the domain of f.(c) Find the range of f.
(Essay)
4.8/5  (47)
(47)
Find the point of intersection of the line x = 2t, y = t - 1, z = 3t + 4 and the plane x - 5y + 3z = 47.
(Multiple Choice)
4.8/5  (34)
(34)
Find an equation of the set of all points P such that the distance from P to A(0, 0, 0) is twice the distance from P to B(0, 0, 1). Describe the set.
(Essay)
4.8/5  (39)
(39)
Given a quadric surface .(a) Identify and sketch the surface.(b) Find the coordinates of the point(s) of intersection of the line passing through the points and and the surface.
(Essay)
4.8/5  (36)
(36)
Find an equation of the plane through the point P = (2, 1, -4) and perpendicular to the line x = 2 + 3t, y = 1 - 4t, z = 3 + 3t.
(Essay)
4.9/5  (46)
(46)
Find the value d for which the plane x - y + 2z = d passes through the point (1, 2, 3).
(Multiple Choice)
4.8/5  (47)
(47)
Find a unit vector that has the same direction as the vector .
(Multiple Choice)
4.8/5  (32)
(32)
Describe the surface whose equation in cylindrical coordinates is .
(Multiple Choice)
4.9/5  (42)
(42)
Find the cosine of the acute angle between the two diagonals of a rectangle with length 3 and width 2.
(Multiple Choice)
4.8/5  (38)
(38)
Given a triangle with vertices A(1, 2), B(2, 3), and C(5, 2), find the angle correct to the nearest degree.
(Short Answer)
4.8/5  (35)
(35)
Showing 21 - 40 of 269
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)