Exam 2: Limits and Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
If a ball is thrown into the air with a velocity of 80 ft/s, its height in feet after t seconds is given by s(t) = 80t - 16t2. It will be at maximum height when its instantaneous velocity is zero. Find its average velocity from the time it is thrown (t = 0) to the time it reaches its maximum height.
(Multiple Choice)
4.9/5  (32)
(32)
Given the graph of below, select a graph which could be that of y = f (x). 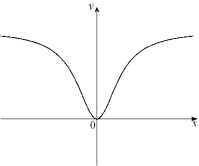
(Multiple Choice)
4.9/5  (34)
(34)
A car on a test track accelerates from 0 ft/s to 208 ft/s in 8 seconds. The car's velocity is given in the table below:
t(s) 0 1 2 3 4 5 6 7 8 v(t)(ft/s) 0 18 47 77 104 132 163 184 208
(a) Find the car's average acceleration for the following time intervals:
(i) [4; 6]
(ii) [4; 5]
(iii) [3; 4]
(b) Estimate the car's acceleration at t = 4.
(Essay)
4.9/5  (36)
(36)
Consider the function Make an appropriate table of values in order to determine the indicated limits:
(a) (b) (c) Does exist? If so, what is its value? If not, explain.
(Essay)
4.9/5  (37)
(37)
A weight is attached to a spring. Suppose the position (in meters) of the weight above the floor t seconds after it is released is given by (a) What is the position of the weight when t = 2? When t = 3? When t = 4?
(b) What is the average rate of change of the position of the weight (in m/s) over the time interval [2, 4]? Over the time interval [2, 3]?
(c) The average rate of change of the position of the weight over the time period [2; 6] is 0. Does this mean that the weight has come to a stop? Why or why not?
(Essay)
4.9/5  (38)
(38)
Find the constant(s) c that make(s) the function continuous on .
(Multiple Choice)
4.8/5  (25)
(25)
Given the graph of y = f (x) below, select a graph which best represents the graph of 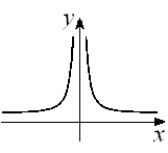
(Multiple Choice)
4.7/5  (34)
(34)
The point lies on the curve Let Q be the point (a) What is the slope of the secant line PQ (correct to 6 decimal places) for the following values of x?
(i) 2
(ii) 1.5
(iii) 1.1
(iv) 1.01
(v) 1.001
(vi) 0
(vii) 0.5
(viii) 0.9
(ix) 0.99
(x) 0.999
(b) Use your results from part (a) to estimate the slope of the tangent line to the graph of
(Essay)
4.7/5  (33)
(33)
Given the following information about limits, select a graph which could be the graph of y = f (x). f(x)=f(x)=0f(x)=f(x)=\infty f(x)=f(x)=-\infty
(Multiple Choice)
4.9/5  (43)
(43)
Given the following information about limits, select a graph which could be the graph of y = f (x). f(x)=f(x)=0f(x)=f(x)=\infty f(x)=f(x)=-\infty
(Multiple Choice)
4.9/5  (36)
(36)
Using the graph below, determine the following: 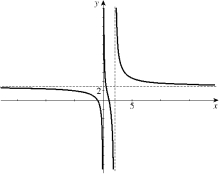 (a) (b) (c) (d) (e) (f) (g) Find the horizontal asymptote(s) of the graph of y = f (x).(h) Find the vertical asymptote(s) of the graph of y = f (x).
(a) (b) (c) (d) (e) (f) (g) Find the horizontal asymptote(s) of the graph of y = f (x).(h) Find the vertical asymptote(s) of the graph of y = f (x).
(Essay)
4.9/5  (32)
(32)
The definition of continuity of f (x) at a point requires three things. List these three conditions, and in each case give an example (a graph or a formula) which illustrates how this condition can fail at x = a.
(Essay)
4.9/5  (36)
(36)
At what value(s) of x does the function have a removable discontinuity?
(Multiple Choice)
5.0/5  (41)
(41)
Showing 21 - 40 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)