Exam 2: Limits and Derivatives
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
If f (x) = 5, which of the following represents
A)
B)3
C)
E)
D)5
F)
G)Does not exist
H)None of the above
(Short Answer)
4.7/5  (39)
(39)
Given the following information about limits, sketch a graph which could be the graph of y = f (x). Label all horizontal and vertical asymptotes. f(x)=f(x)=-1,f(x)=f(x)=-\infty f(x)=f(x)=\infty, and f=(0)=1
(Essay)
4.8/5  (36)
(36)
Given that find the following limits, if they exist. If a limit does not exist, explain why.(a) (b) (c) (d) (e) (f) (g) (h)
(Essay)
4.8/5  (40)
(40)
Find an equation of the line tangent to the curve y = x + (1/x) at the point
(Multiple Choice)
4.8/5  (46)
(46)
Find the derivative of f (x) = 3x - 5 using the definition of the derivative.
(Essay)
4.8/5  (40)
(40)
Use the given graph to find the indicated quantities: 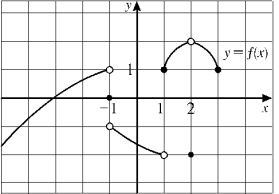 (a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) (i)
(j) f (-1)
(k) f (0)
(l) f (1)
(m) f (2)
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) (i)
(j) f (-1)
(k) f (0)
(l) f (1)
(m) f (2)
(Essay)
4.9/5  (33)
(33)
Find the distance between the two values of x at which the function is discontinuous.
(Multiple Choice)
4.9/5  (38)
(38)
Given the graph of y = f (x), sketch the graph of y = (a) 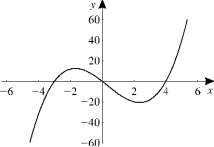 (b)
(b) 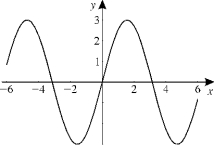 (c)
(c) 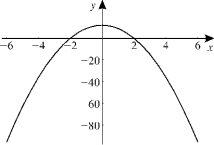 (d)
(d) 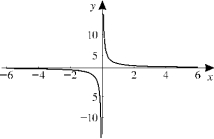
(Essay)
4.9/5  (41)
(41)
Below are the graphs of a function and its first and second derivatives. Identify which of the following graphs (a, b, and c) is f (x), which is , and which is . Justify your choices. 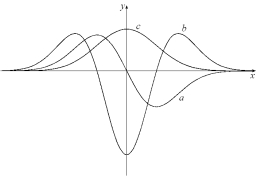
(Essay)
4.9/5  (35)
(35)
In order to determine an appropriate delivery schedule to a group of rural homes in North Dakota, a fuel oil distributor monitors fuel oil consumption and the daily outdoor temperature (in degrees Fahrenheit). A table was constructed for a function F (T) of fuel oil consumption (in gallons per day) as a function of the temperature T.(a) Sketch a graph which you believe would approximate the graph of y = F (T).(b) What is the meaning of What are its units?
(c) Write a sentence that would explain to an intelligent layperson the meaning of
(Essay)
4.8/5  (36)
(36)
The displacement in meters of a particle moving in a straight line is given by s = t3, where t is measured in seconds. Find the average velocity in meters per second over the time period [1, 2].
(Multiple Choice)
5.0/5  (38)
(38)
For each of the following problems, make an appropriate table to determine the limits.(a) (b) (c)
(Essay)
4.9/5  (27)
(27)
For the curve f(x) = , find the slope MPQ of the secant line through the points P = (1, f (1)) and Q = (6, f (6)).
(Multiple Choice)
4.8/5  (38)
(38)
Suppose that the height of a projectile red vertically upward from a height of 80 feet with an initial velocity of 64 feet per second is given by h (t) = -16t2 + 64t + 80.(a) Compute the height of the object for t = 0, 1, 2, 3, 4, 5, and 6 seconds.(b) What is the physical significance of h (6)? What does that suggest about the domain of h?
(c) What is the average velocity of the projectile for each of the following time intervals?
(i) [1; 3]
(ii) [0; 2]
(iii) [0; 4]
(d) What is the physical significance of an average velocity of 0?
(e) When does the projectile reach its maximum height?
(f) For what value(s) of t is h (t) = 0? Are all solutions to the equation valid? Explain.
(Essay)
4.8/5  (42)
(42)
A weight is attached to a spring. Suppose the position (in meters) of the weight above the floor t seconds after it is released is given by . What is the average rate of change of the position of the weight (in m/s) over the time interval [3, 5]?
(Multiple Choice)
4.8/5  (38)
(38)
If f (-1) = 3 and , find an equation of the tangent line at x = -1.
(Multiple Choice)
4.9/5  (35)
(35)
Given the graph of y = f (x), find all values of x for which
(a) (b) (c) (d) 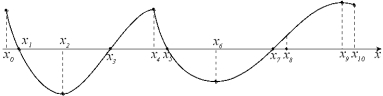
(Essay)
4.8/5  (30)
(30)
Showing 81 - 100 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)