Exam 14: Simple Linear Regression
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays62 Questions
Exam 3: Descriptive Statistics: Numerical Measures173 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions123 Questions
Exam 6: Continuous Probability Distributions174 Questions
Exam 7: Sampling and Sampling Distributions133 Questions
Exam 8: Interval Estimation137 Questions
Exam 9: Hypothesis Tests148 Questions
Exam 10: Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances90 Questions
Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit90 Questions
Exam 13: Experimental Design and Analysis of Variance115 Questions
Exam 14: Simple Linear Regression146 Questions
Exam 15: Multiple Regression115 Questions
Exam 16: Regression Analysis: Model Building76 Questions
Exam 17: Time Series Analysis and Forecasting68 Questions
Exam 18: Nonparametric Methods81 Questions
Exam 19: Statistical Methods for Quality Control29 Questions
Exam 20: Index Numbers52 Questions
Exam 21: Decision Analysis on Website65 Questions
Exam 22: Sample Survey on Website63 Questions
Select questions type
In a regression analysis, the coefficient of correlation is 0.16. The coefficient of determination in this situation is
(Multiple Choice)
4.9/5  (34)
(34)
Regression analysis was applied between demand for a product (Y) and the price of the product (X), and the following estimated regression equation was obtained. 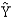 = 120 - 10 X Based on the above estimated regression equation, if price is increased by 2 units, then demand is expected to
= 120 - 10 X Based on the above estimated regression equation, if price is increased by 2 units, then demand is expected to
(Multiple Choice)
4.8/5  (22)
(22)
The following sample data contains the number of years of college and the current annual salary for a random sample of heavy equipment salespeople. 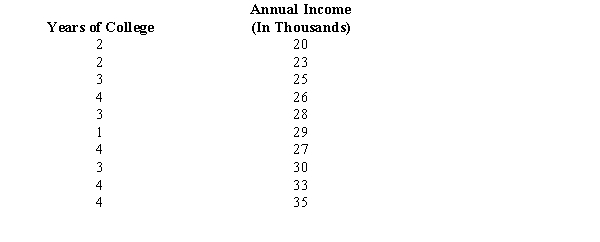 a. Which variable is the dependent variable? Which is the independent variable?
b. Determine the least squares estimated regression line.c. Predict the annual income of a salesperson with one year of college.d. Test if the relationship between years of college and income is statistically significant at the .05 level of significance.e. Calculate the coefficient of determination.
f. Calculate the sample correlation coefficient between income and years of college. Interpret the value you obtain.
a. Which variable is the dependent variable? Which is the independent variable?
b. Determine the least squares estimated regression line.c. Predict the annual income of a salesperson with one year of college.d. Test if the relationship between years of college and income is statistically significant at the .05 level of significance.e. Calculate the coefficient of determination.
f. Calculate the sample correlation coefficient between income and years of college. Interpret the value you obtain.
(Essay)
4.8/5  (43)
(43)
The model developed from sample data that has the form of 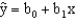 is known as
is known as
(Multiple Choice)
4.8/5  (36)
(36)
If the coefficient of determination is 0.9, the percentage of variation in the dependent variable explained by the variation in the independent variable
(Multiple Choice)
4.9/5  (37)
(37)
Regression analysis was applied between sales (in $1000) and advertising (in $100) and the following regression function was obtained. 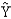 = 500 + 4 X Based on the above estimated regression line if advertising is $10,000, then the point estimate for sales (in dollars) is
= 500 + 4 X Based on the above estimated regression line if advertising is $10,000, then the point estimate for sales (in dollars) is
(Multiple Choice)
4.8/5  (33)
(33)
If the coefficient of correlation is 0.4, the percentage of variation in the dependent variable explained by the variation in the independent variable
(Multiple Choice)
4.8/5  (41)
(41)
If the coefficient of determination is 0.81, the coefficient of correlation
(Multiple Choice)
4.8/5  (29)
(29)
If the coefficient of correlation is -0.4, then the slope of the regression line
(Multiple Choice)
4.8/5  (38)
(38)
Exhibit 14-8
The following information regarding a dependent variable Y and an independent variable X is provided  -Refer to Exhibit 14-8. The total sum of squares (SST) is
-Refer to Exhibit 14-8. The total sum of squares (SST) is
(Multiple Choice)
4.9/5  (36)
(36)
Exhibit 14-8
The following information regarding a dependent variable Y and an independent variable X is provided  -Refer to Exhibit 14-8. The slope of the regression equation is
-Refer to Exhibit 14-8. The slope of the regression equation is
(Multiple Choice)
4.9/5  (28)
(28)
Exhibit 14-4
Regression analysis was applied between sales data (Y in $1,000s) and advertising data (x in $100s) and the following information was obtained. 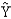 = 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 14-4. The F statistic computed from the above data is
= 12 + 1.8 x
n = 17
SSR = 225
SSE = 75
Sb1 = 0.2683
-Refer to Exhibit 14-4. The F statistic computed from the above data is
(Multiple Choice)
4.7/5  (39)
(39)
Part of an Excel output relating X (independent variable) and Y (dependent variable) is shown below. Fill in all the blanks marked with "?". 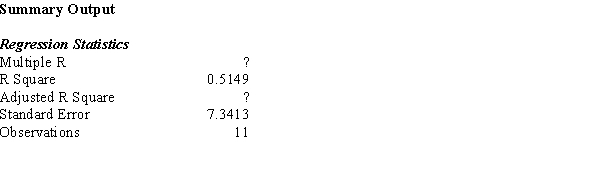

(Essay)
4.9/5  (32)
(32)
Below you are given information on a woman's age and her annual expenditure on purchase of books. 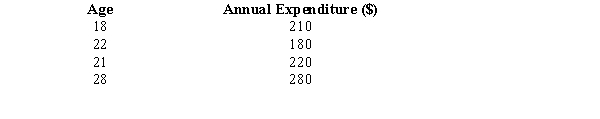 a.Develop the least squares regression equation.
b.Compute the coefficient of determination.
c.Use a t test to determine whether the slope is significantly different from zero. Let = 0.05.
d.At 95% confidence, perform an F test and determine whether or not the model is significant.
a.Develop the least squares regression equation.
b.Compute the coefficient of determination.
c.Use a t test to determine whether the slope is significantly different from zero. Let = 0.05.
d.At 95% confidence, perform an F test and determine whether or not the model is significant.
(Essay)
4.9/5  (32)
(32)
Exhibit 14-8
The following information regarding a dependent variable Y and an independent variable X is provided  -Refer to Exhibit 14-8. The sum of squares due to error (SSE) is
-Refer to Exhibit 14-8. The sum of squares due to error (SSE) is
(Multiple Choice)
4.9/5  (41)
(41)
Researchers have collected data on the hours of television watched in a day and the age of a person. You are given the data below. 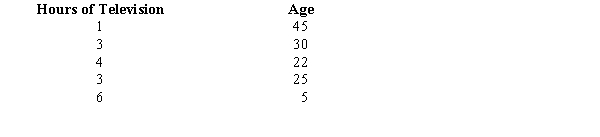 a.Determine which variable is the dependent variable.
b.Compute the least squares estimated line.
c.Is there a significant relationship between the two variables? Use a .05 level of significance. Be sure to state the null and alternative hypotheses.
d.Compute the coefficient of determination. How would you interpret this value?
a.Determine which variable is the dependent variable.
b.Compute the least squares estimated line.
c.Is there a significant relationship between the two variables? Use a .05 level of significance. Be sure to state the null and alternative hypotheses.
d.Compute the coefficient of determination. How would you interpret this value?
(Essay)
4.8/5  (38)
(38)
A regression and correlation analysis resulted in the following information regarding an independent variable (x) and a dependent variable (y).
X = 42
(Y - 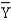 )(X -
)(X - 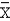 ) = 37
Y = 63
(X -
) = 37
Y = 63
(X - 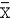 )2 = 84
n = 7
(Y -
)2 = 84
n = 7
(Y - 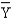 )2 = 28
)2 = 28 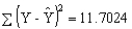 a.Develop the least squares estimated regression equation.
b.At 95% confidence, perform a t test and determine whether or not the slope is significantly different from zero.
c.Perform an F test to determine whether or not the model is significant. Let = 0.05.
d.Compute the coefficient of determination.
a.Develop the least squares estimated regression equation.
b.At 95% confidence, perform a t test and determine whether or not the slope is significantly different from zero.
c.Perform an F test to determine whether or not the model is significant. Let = 0.05.
d.Compute the coefficient of determination.
(Essay)
4.7/5  (32)
(32)
Exhibit 14-3
You are given the following information about y and x.  -Refer to Exhibit 14-3. The coefficient of determination equals
-Refer to Exhibit 14-3. The coefficient of determination equals
(Multiple Choice)
4.9/5  (26)
(26)
Showing 61 - 80 of 146
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)