Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit

Exhibit 12-7 You want to test whether or not the following sample of 30 observations follows a normal distribution. The mean of the sample equals 11.83, and the standard deviation equals 4.53. 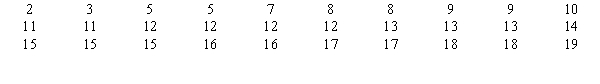-Refer to Exhibit 12-7. The calculated value for the test statistic equals

Before the start of the Winter Olympics, it was expected that the percentages of medals awarded to the top contenders to be as follows. 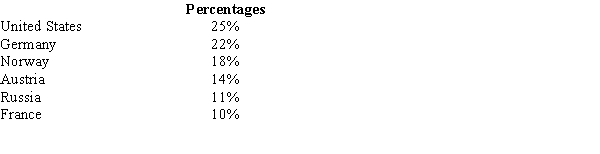Midway through the Olympics, of the 120 medals awarded, the following distribution was observed. We want to test to see if there is a significant difference between the expected and actual awards given. a.Compute the test statistic. b.Using the p-value approach, test to see if there is a significant difference between the expected and the actual values. Let $\alpha$ = .05. c.At 95% confidence, test for a significant difference using the critical value approach.

Exhibit 12-2 Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification. We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. -Refer to Exhibit 12-2. The calculated value for the test statistic equals

The data below represents the fields of specialization for a randomly selected sample of undergraduate students. We want to determine whether there is a significant difference in the fields of specialization between regions of the country. 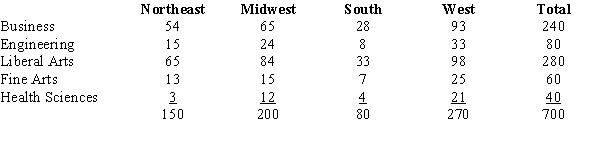a.Determine the critical value of the chi-square $\chi$ ² for this test of independence. b.Calculate the value of the test statistic. c.What is the conclusion for this test? Let $\alpha$ = .05.

A major automobile manufacturer claimed that the frequencies of repairs on all five models of its cars are the same. A sample of 200 repair services showed the following frequencies on the various makes of cars. At $\alpha$ = 0.05, test the manufacturer's claim.

Exhibit 12-7 You want to test whether or not the following sample of 30 observations follows a normal distribution. The mean of the sample equals 11.83, and the standard deviation equals 4.53. 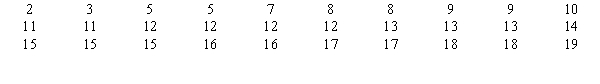-Refer to Exhibit 12-7. The number of intervals or categories used to test the hypothesis for this problem is

Exhibit 12-1 When individuals in a sample of 150 were asked whether or not they supported capital punishment, the following information was obtained. We are interested in determining whether or not the opinions of the individuals (as to Yes, No, and No Opinion) are uniformly distributed. -Refer to Exhibit 12-1. The conclusion of the test (at 95% confidence) is that the

Exhibit 12-3 In order to determine whether or not a particular medication was effective in curing the common cold, one group of patients was given the medication, while another group received sugar pills. The results of the study are shown below. 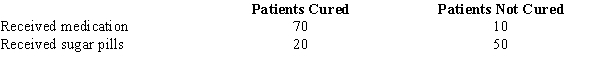We are interested in determining whether or not the medication was effective in curing the common cold. -Refer to Exhibit 12-3. The test statistic is

Before the presidential debates, it was expected that the percentages of registered voters in favor of various candidates would be as follows. 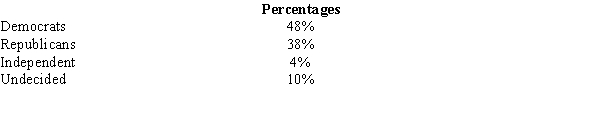After the presidential debates, a random sample of 1200 voters showed that 540 favored the Democratic candidate; 480 were in favor of the Republican candidate; 40 were in favor of the Independent candidate, and 140 were undecided. We want to see if the proportion of voters has changed. a.Compute the test statistic. b.Use the p-value approach to test the hypotheses. Let $\alpha$ = .05. c.Using the critical value approach, test the hypotheses. Let $\alpha$ = .05.

Exhibit 12-4 In the past, 35% of the students at ABC University were in the Business College, 35% of the students were in the Liberal Arts College, and 30% of the students were in the Education College. To see whether or not the proportions have changed, a sample of 300 students was taken. Ninety of the sample students are in the Business College, 120 are in the Liberal Arts College, and 90 are in the Education College. -Refer to Exhibit 12-4. The conclusion of the test is that the

Exhibit 12-5 The table below gives beverage preferences for random samples of teens and adults. We are asked to test for independence between age (i.e., adult and teen) and drink preferences. -Refer to Exhibit 12-5. The expected number of adults who prefer coffee is

Use $\alpha$ = 0.05 to determine if the following sample comes from a normal distribution. Use the critical value approach.

A lottery is conducted that involves the random selection of numbers from 0 to 4. To make sure that the lottery is fair, a sample of 250 was taken. The following results were obtained: a.State the null and alternative hypotheses to be tested. b.Compute the test statistic. c.The null hypothesis is to be tested at the 5% level of significance. Determine the critical value from the table. d.What do you conclude about the fairness of this lottery?

Exhibit 12-7 You want to test whether or not the following sample of 30 observations follows a normal distribution. The mean of the sample equals 11.83, and the standard deviation equals 4.53. 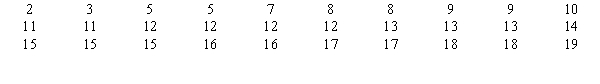-Refer to Exhibit 12-7. At 95% confidence, the conclusion of the test is that the

A manager believes that the shelf life of apple juice is normally distributed. A sample of 30 containers of juice was taken and the shelf life was recorded. You are given the results below. The average shelf life in the sample was 23.07 days with a standard deviation of 4.29 days. a.State the null and alternative hypotheses. b.Compute the test statistic for the goodness of fit test. c.At 95% confidence using the p-value approach, test the hypotheses. What do you conclude about the distribution?

Prior to the start of the season, it was expected that audience proportions for the four major news networks would be CBS 28%, NBC 35%, ABC 22% and BBC 15%. A recent sample of homes yielded the following viewing audience data. We want to determine whether or not the recent sample supports the expectations of the number of homes of the viewing audience of the four networks. a.State the null and alternative hypotheses to be tested. b.Compute the test statistic. c.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test. d.What do you conclude?

Last school year, in the school of Business Administration, 30% were Accounting majors, 24% Management majors, 26% Marketing majors, and 20% Economics majors. A sample of 300 students taken from this year's students of the school showed the following number of students in each major: We want to see if there has been a significant change in the number of students in each major. a.Compute the test statistic. b.Has there been any significant change in the number of students in each major between the last school year and this school year. Use the p-value approach and let $\alpha$ = .05.

Exhibit 12-2 Last school year, the student body of a local university consisted of 30% freshmen, 24% sophomores, 26% juniors, and 20% seniors. A sample of 300 students taken from this year's student body showed the following number of students in each classification. We are interested in determining whether or not there has been a significant change in the classifications between the last school year and this school year. -Refer to Exhibit 12-2. The expected number of freshmen is

Exhibit 12-8 The following shows the number of individuals in a sample of 300 who indicated they support the new tax proposal. 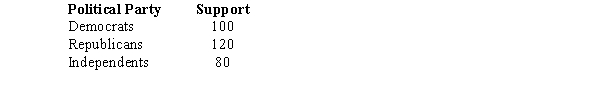We are interested in determining whether or not the opinions of the individuals of the three groups are uniformly distributed. -Refer to Exhibit 12-8. The calculated value for the test statistic equals

Exhibit 12-6 The owner of a car wash wants to see if the arrival rate of cars follows a Poisson distribution. In order to test the assumption of a Poisson distribution, a random sample of 150 ten-minute intervals was taken. You are given the following observed frequencies: -Refer to Exhibit 12-6. The calculated value for the test statistic equals