Exam 12: Comparing Multiple Proportions, Test of Independence and Goodness of Fit

A statistical test conducted to determine whether to reject or not reject a hypothesized probability distribution for a population is known as a

Shown below is 2 x 3 contingency table with observed values from a sample of 500. At 95% confidence using the critical value approach, test for independence of the row and column factors.

The number of degrees of freedom for the appropriate chi-square distribution in a test of independence is

A sample of 150 individuals (males and females) was surveyed, and the individuals were asked to indicate their yearly incomes. Their incomes were categorized as follows. 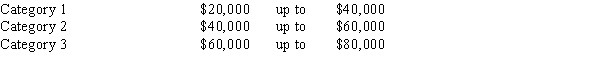The results of the survey are shown below. 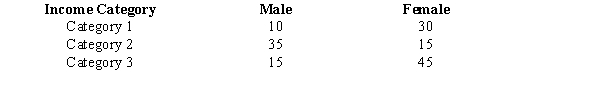We want to determine if yearly income is independent of gender. a.Compute the test statistic. b.Using the p-value approach, test to determine if yearly income is independent of gender.

Shoppers were asked where they do their regular grocery shopping. The table below shows the responses of the sampled shoppers. We are interested in determining if the proportions of females in the three categories are different from each other. 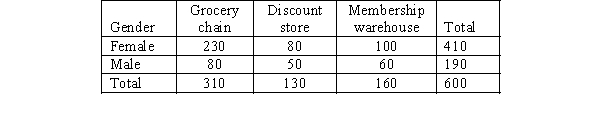a.Provide the null and the alternative hypotheses. b.Determine the expected frequencies. c.Compute the sample proportions. d.Compute the critical values (CV_ij). e.Give your conclusions by providing numerical reasoning.

If there are three or more populations, then it is

The results of a recent study regarding smoking and three types of illness are shown in the following table. 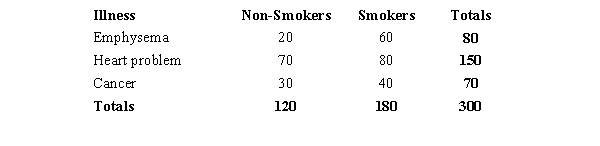We are interested in determining whether or not illness is independent of smoking. a.State the null and alternative hypotheses to be tested. b.Show the contingency table of the expected frequencies. c.Compute the test statistic. d.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test. What do you conclude? e.Determine the p-value and perform the test.

In the last presidential election, before the candidates started their major campaigns, the percentages of registered voters who favored the various candidates were as follows. After the major campaigns began, a random sample of 400 voters showed that 172 favored the Republican candidate; 164 were in favor of the Democratic candidate; and 64 favored the Independent candidate. We are interested in determining whether the proportion of voters who favored the various candidates had changed. a.Compute the test statistic. b.Using the p-value approach, test to see if the proportions have changed. c.Using the critical value approach, test the hypotheses.

An insurance company has gathered the following information regarding the number of accidents reported per day over a period of 100 days. 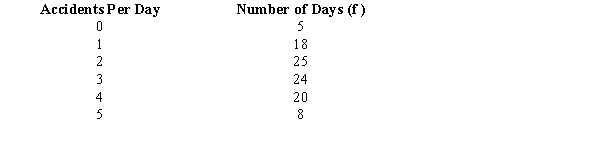Using the critical value approach test to see if the above data have a Poisson distribution. Let $\alpha$ = 0.05.

Five hundred randomly selected automobile owners were questioned on the main reason they had purchased their current automobile. The results are given below. 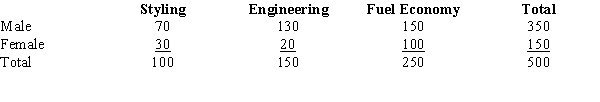a.State the null and alternative hypotheses for a contingency table test. b.State the decision rule for the critical value approach. Let $\alpha$ = .01. c.Calculate the $\chi$ ² test statistic. d.Give your conclusion for this test.