Exam 18: Line Integrals
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Let be the vector field shown below. 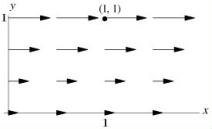 Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?
Let C be the rectangular loop from (0, 0)to (1, 0)to (1, 1)to (0, 1), then back to (0, 0). Do you expect the line integral to be positive, negative or zero?
(Multiple Choice)
4.8/5  (38)
(38)
Let and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
Find
(Short Answer)
4.7/5  (31)
(31)
Find a vector field with the property that the line integral of along the line from (0, 0)to (a, b)is for any numbers a and b.
(Essay)
4.9/5  (33)
(33)
Use Green's Theorem to find the line integral of around the closed curve composed of the graph of y = x2n where n is a positive integer and the line y = 1.
(Essay)
4.8/5  (36)
(36)
Find the line integral of around the curve consisting of the graph of y = xn from the origin to the point (1, 1), followed by straight lines from (1, 1)to (0, 1)and from (0, 1)back to the origin.
(Essay)
4.8/5  (43)
(43)
Let Find the value of where C is a path joining (0, 0)to the point (1, 2).
(Short Answer)
4.9/5  (42)
(42)
The following table gives values of a function f(x, y).The table reflects the properties of the function, which is differentiable and defined for all (x, y). x y 1 2 3 4 5 6 7 8 9 10 1 7 8 4 3 8 2 1 1 5 9 2 5 9 7 11 7 3 1 4 2 10 3 6 8 14 11 10 5 13 13 12 14 4 11 15 20 22 25 24 21 21 15 12 5 17 25 30 31 32 35 37 40 35 32 6 25 30 34 30 29 26 15 14 12 9 7 39 42 51 55 50 49 47 45 35 36 8 26 21 19 24 28 27 30 33 45 39 9 49 50 55 62 69 71 60 54 49 47 10 65 70 64 6 63 49 42 41 40 38 Let and Find if C is the circle of radius 2 centered at (4, 3).
(Short Answer)
4.7/5  (33)
(33)
On an exam, students were asked to evaluate , where C is the circle centered at the origin of radius r: .One student wrote:
"Since Using Green's Theorem, ."
Do you agree with the student?
(Essay)
4.7/5  (35)
(35)
Let C be the circular path which is the portion of the circle of radius 1 centered at the origin starting at (1, 0)and ending at (0,-1), oriented counterclockwise.
Let Determine the exact value of
(Essay)
4.8/5  (34)
(34)
Calculate when and C is the line from the origin to the point (4, 4, 4).
(Short Answer)
4.9/5  (33)
(33)
Let C be the unit circle oriented in a counter-clockwise direction.Say whether the following statements are true or false.
If , we can conclude that is path-independent field.
(True/False)
5.0/5  (40)
(40)
Calculate the line integral of along a quarter of a circle centered at the origin, starting at (3, 0)and ending at (0, -3).
(Essay)
4.8/5  (36)
(36)
Let and let Ca be the circle of radius a centered at the origin, traveled in a counter-clockwise direction.
Find
(Essay)
4.8/5  (29)
(29)
If , compute where C is the curve from A(0, 0, 3)to B(2, 1, 5)shown below.
Hint: messy computation can be avoided. 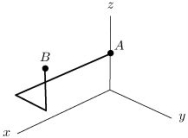
(Short Answer)
4.9/5  (35)
(35)
Suppose that and where C1 is the line joining (0, 0)to (1, 0), C2 is the line joining (0, 0)to (3, 0), C3 is the line joining (0, 0)to (0, 1)and C4 is the line joining (0, 1)to (0, 2).
Determine, if possible, the value of the line integral of along the line from (0, 1)to (1, 0).If the value cannot be determined, say so.
(Short Answer)
4.9/5  (36)
(36)
Let Ca be the circle x2 + y2 = a2 oriented counter-clockwise.
Use Green's theorem to find
(Essay)
4.8/5  (33)
(33)
Let C be the unit circle oriented in a counter-clockwise direction.Say whether the following statements are true or false.If , we can conclude that is not path-independent field.
(True/False)
4.8/5  (37)
(37)
Suppose that and .
Estimate the work done by along the line from (1, 0)to (1, 1).
(Short Answer)
4.8/5  (39)
(39)
Use Green's Theorem to calculate the circulation of around the triangle with vertices (0, 0), (1, 0)and (0, 1), oriented counter-clockwise.
(Essay)
4.9/5  (35)
(35)
Showing 21 - 40 of 78
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)