Exam 18: Line Integrals
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Use Green's Theorem to evaluate where C is the circle of radius centered at oriented in a counter-clockwise direction.
(Essay)
4.7/5  (36)
(36)
Given the graph of the vector field, , shown below, list the following quantities in increasing order: 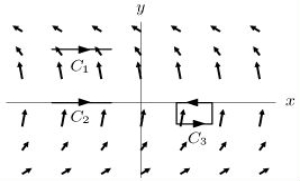
(Essay)
4.8/5  (33)
(33)
Evaluate , where C is the curve for 0 t 1.
Note that the line integral is around -C, not C.
(Short Answer)
4.9/5  (46)
(46)
Explain in words and symbols how to calculate the line integral given a parameterization, of the curve C.
(Essay)
4.8/5  (40)
(40)
Let and be two 2-dimensional fields, where and Let C1 be the circle with center (2, 2)and radius 1 oriented counterclockwise.
Let C2 be the path consisting of the straight line segments from (0, 4)to (0, 1)and from (0, 1)to (3, 1).
Find the line integral Use "pi" to represent if necessary.
(Short Answer)
4.8/5  (39)
(39)
If the length of curve C1 is longer than the length of curve C2, then
(True/False)
4.8/5  (38)
(38)
Let f(x, y, z)be a function of three variables.Suppose that C is an oriented curve lying on the level surface f(x, y, z)= 2.
Find the line integral
(Short Answer)
4.9/5  (35)
(35)
If is a path-independent field, then where C has the parameterization
(True/False)
4.7/5  (32)
(32)
Let be the constant vector field Calculate the line integral of along a line segment L of length 9 at an angle /3 to
(Short Answer)
4.8/5  (32)
(32)
Consider the vector field .
Without using parametrization, calculate directly the line integral of along the line from (3, 3)to (7, 3).
(Short Answer)
4.7/5  (39)
(39)
Suppose a curve C is parameterized by with and suppose is a vector field for .Explain why
(Essay)
4.8/5  (32)
(32)
Let be a vector field with constant magnitude Suppose that 0 t 5, is a parameterization of a flow line C of .
Find
(Short Answer)
5.0/5  (42)
(42)
State the Fundamental Theorem of Calculus for Line Integrals.
(Multiple Choice)
4.9/5  (44)
(44)
Let Use the curl test to check whether is path-independent.
(Multiple Choice)
4.8/5  (42)
(42)
Showing 61 - 78 of 78
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)