Exam 17: Parameterization and Vector Fields
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Consider the curve Find the equation of the tangent line at the point where t = 2.
(Essay)
4.9/5  (32)
(32)
The equation parameterizes a line through the point (4, 3, 7).
What is the value of t at this point?
(Short Answer)
4.9/5  (30)
(30)
Find a parameterization of a curve that looks like sin y = z when viewed from the x-axis, and looks like x = z2 when viewed from the y-axis.See the shadows drawn on the planes in the following picture. 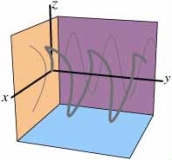 What does the curve look like when viewed from the z-axis?
What does the curve look like when viewed from the z-axis?
(Essay)
4.9/5  (37)
(37)
Describe the similarities and differences between the following two curves.
(Essay)
4.9/5  (36)
(36)
A particle moves at a constant speed along a line through P = (10,-20, 22)and Q = (22, -46, 46).Find a parametric equation for the line if the particle passes through P at time t = 3 and passes through Q at time t = 7.
(Essay)
4.9/5  (39)
(39)
For the following vector field, identify which one of the following formulas could represent it. The scales in the x and y directions are the same.No reasons need be given. 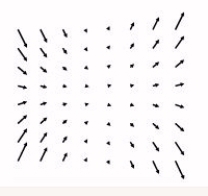
(Multiple Choice)
4.9/5  (33)
(33)
Showing 81 - 86 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)