Exam 17: Parameterization and Vector Fields
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Let f(x, y)be a function that depends on only one of the variables, that is, of the form f(x, y)= g(x)or f(x, y)= g(y). Could the following picture be the gradient of f? 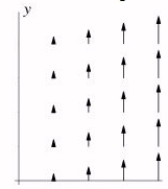
(Multiple Choice)
4.8/5  (38)
(38)
Write a formula for a vector field whose vectors are parallel to the x-axis and point away from the y-axis, with magnitude inversely proportional to the cube of the distance from the x-axis.
(Essay)
4.7/5  (35)
(35)
Parameterize the curve which lies on the plane 5x - 10y + z = 6 above the circle
(Multiple Choice)
4.7/5  (31)
(31)
Find a parametric equation for the line which passes through the point (5, 1, -1)and is parallel to the line .
(Essay)
4.8/5  (41)
(41)
Give parameterizations for a circle of radius 2 in the plane, centered at origin, traversed anticlockwise.
(Multiple Choice)
4.9/5  (35)
(35)
A particle moves with position vector . Describe the movement of the particle as t .
(Multiple Choice)
4.7/5  (34)
(34)
Let S be a circular cylinder of radius 0.2, such that the center of one end is at the origin and the center of the other end is at the point (5, 0, 4).
Find the xyz-equation of the plane, P, containing the base of the cylinder (i.e., the plane through the origin perpendicular to the axis of the cylinder).
(Essay)
4.8/5  (38)
(38)
Find a parameterization of the curve and use it to calculate the path length of this curve from (0, 0)to (1, 1).
(Short Answer)
4.9/5  (34)
(34)
The line through the points (2, 5, 25)and (12, 7, 23)can be parameterized by .
What value of t gives the point (42, 13, 17)?
(Short Answer)
4.8/5  (32)
(32)
The path of an object moving in xyz-space is given by The temperature at a point (x,y,z)in space is given by .
(a)At time , what is the object's velocity ? What is its speed?
(b)Calculate the directional derivative of f in the direction of at the point (1,2,1), where is the velocity vector you found in part (a).
(c)Calculate (d)Explain briefly how your answers to part (a), (b)and (c)are related.Interpret them in terms of temperature.
(Essay)
4.8/5  (35)
(35)
Consider the curve .
(a)Find a unit vector tangent to the curve at the point (1,2,3).
(b)Show that the curve lies on the surface .
(Essay)
4.9/5  (39)
(39)
In an exam, students are asked to find the arc length of the curve C parameterized by , for .
One student wrote the following
" Thus the arc length is "
This answer cannot be true.
(a)Which part of the student's calculation was wrong?
(b)Find the correct answer.
(Essay)
4.9/5  (37)
(37)
Answer the following as "true", "false" or "need more information".
If a particle moves with velocity , then the particle stops at the origin.
(Short Answer)
4.9/5  (38)
(38)
Consider the parametric surface Does it contain the point (0, -3, -4)?
(True/False)
4.8/5  (36)
(36)
What curve, C, is traced out by the parameterization for ? Give a very complete verbal description.
(Essay)
4.9/5  (38)
(38)
Find the parametric equations for the line of the intersection of the planes and .
(Essay)
4.8/5  (40)
(40)
Which of the following equations give alternate parameterizations of the line L parameterized by
(Multiple Choice)
4.8/5  (28)
(28)
If the flow lines for the vector field are all concentric circles centered at the origin, then for all
(True/False)
4.9/5  (39)
(39)
Suppose
Find a function f(x, y, z) of three variables with the property that the vectors in on a level surface of f (x, y, z) are perpendicular to the level surface of f(x, y, z) at each point.
(Essay)
4.9/5  (43)
(43)
Showing 41 - 60 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)