Exam 8: Momentum, Impulse, and Collisions
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Equilibrium: In the figure, a 10.0-m long bar is attached by a frictionless hinge to a wall and held horizontal by a rope that makes an angle θ of 53° with the bar. The bar is uniform and weighs 39.9 N. How far from the hinge should a 10.0-kg mass be suspended for the tension T in the rope to be 125 N? 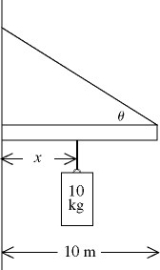
(Short Answer)
4.8/5  (46)
(46)
Rotational dynamics about a fixed axis: In the figure, a very light rope is wrapped around a wheel of radius R = 2.0 meters and does not slip. The wheel is mounted with frictionless bearings on an axle through its center. A block of mass 14 kg is suspended from the end of the rope. When the system is released from rest it is observed that the block descends 10 meters in 2.0 seconds. What is the moment of inertia of the wheel? 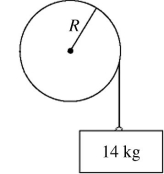
(Short Answer)
4.9/5  (47)
(47)
Equilibrium: In the figure, a uniform rectangular crate 0.40 m wide and 1.0 m tall rests on a horizontal surface. The crate weighs 930 N, and its center of gravity is at its geometric center. A horizontal force F is applied at a distance h above the floor. If 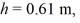 what minimum value of F is required to make the crate start to tip over? Static friction is large enough that the crate does not start to slide.
what minimum value of F is required to make the crate start to tip over? Static friction is large enough that the crate does not start to slide. 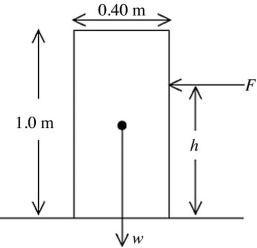
(Short Answer)
4.9/5  (32)
(32)
Torque: What is the torque about the origin on a particle located at 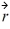 = 3 m
= 3 m  + 4 m
+ 4 m  - 2 m
- 2 m  if a force
if a force 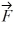 = 5N
= 5N  - 2 N
- 2 N  + 3 N
+ 3 N  on the particle?
on the particle?
(Multiple Choice)
4.8/5  (33)
(33)
Rolling: A tire is rolling along a road, without slipping, with a velocity v. A piece of tape is attached to the tire. When the tape is opposite the road (at the top of the tire), its velocity with respect to the road is
(Multiple Choice)
4.9/5  (37)
(37)
Rotational dynamics about a moving axis: A uniform hollow spherical ball of mass 1.75 kg and radius 40.0 cm rolls without slipping up a ramp that rises at 30.0° above the horizontal. The speed of the ball at the base of the ramp is 2.63 m/s. While the ball is moving up the ramp, find
(a) the acceleration (magnitude and direction) of its center of mass and
(b) the friction force (magnitude and direction) acting on it due to the surface of the ramp.
(Essay)
4.9/5  (32)
(32)
Rotational kinetic energy: While spinning down from 500.0 rpm to rest, a solid uniform flywheel does 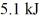 of work. If the radius of the disk is
of work. If the radius of the disk is 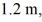 what is its mass?
what is its mass?
(Multiple Choice)
4.8/5  (40)
(40)
Rolling: Consider a uniform solid sphere of radius R and mass M rolling without slipping. Which form of its kinetic energy is larger, translational or rotational?
(Multiple Choice)
4.7/5  (33)
(33)
Rotational kinematics with constant angular acceleration: In the figure, point P is at rest when it is on the x-axis. The time t, when P returns to the original position on the x-axis, is closest to 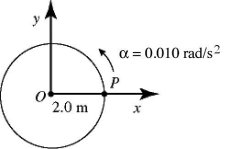
(Multiple Choice)
4.8/5  (39)
(39)
Rotational dynamics about a fixed axis: For the apparatus shown in the figure, there is no slipping between the cord and the surface of the pulley. The blocks have mass of 3.0 kg and 5.7 kg, and the pulley has a radius of 0.12 m and a mass of 10.3 kg. At the instant the 5.7 kg mass has fallen 1.5 m starting from rest, find the speed of each block. (Assume the pulley is in the shape of a uniform solid disk and has no friction in its axle.) 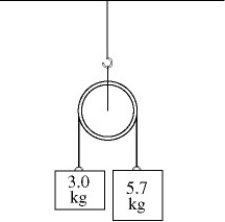
(Short Answer)
4.8/5  (33)
(33)
Equilibrium: A uniform 300-kg beam, 6.00 m long, is freely pivoted at P, as shown in the figure. The beam is supported in a horizontal position by a light strut, 5.00 m long, which is freely pivoted at Q and is loosely pinned to the beam at R. A load of mass is suspended from the end of the beam at S. A maximum compression of 23,000 N in the strut is permitted, due to safety. Under maximum load, find the magnitude of the x component of the force exerted on the beam by the pivot at P. 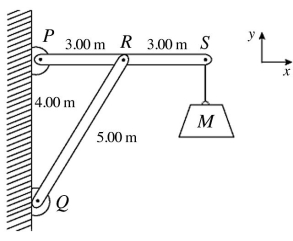
(Multiple Choice)
4.8/5  (38)
(38)
Rotational dynamics about a fixed axis: A string is wrapped around a pulley with a radius of 2.0 cm and no appreciable friction in its axle. The pulley is initially not turning. A constant force of 50 N is applied to the string, which does not slip, causing the pulley to rotate and the string to unwind. If the string unwinds 1.2 m in 4.9 s, what is the moment of inertia of the pulley?
(Multiple Choice)
4.9/5  (41)
(41)
Conservation of angular momentum: A metal bar is hanging from a hook in the ceiling when it is suddenly struck by a ball that is moving horizontally (see figure). The ball is covered with glue, so it sticks to the bar. During this collision 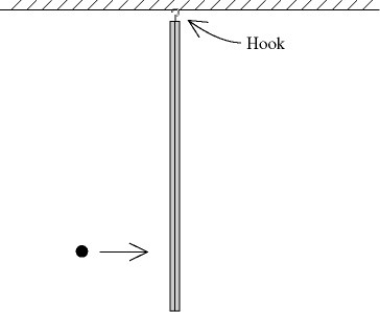
(Multiple Choice)
4.8/5  (36)
(36)
Rotational dynamics about a fixed axis: A 72.0-kg person pushes on a small doorknob with a force of 5.00 N perpendicular to the surface of the door. The doorknob is located 0.800 m from axis of the frictionless hinges of the door. The door begins to rotate with an angular acceleration of 2.00 rad/s2. What is the moment of inertia of the door about the hinges?
(Multiple Choice)
4.9/5  (40)
(40)
Conservation of angular momentum: A figure skater rotating at 5.00 rad/s with arms extended has a moment of inertia of 2.25 kg ∙ m2. If the arms are pulled in so the moment of inertia decreases to 1.80 kg ∙ m2, what is the final angular speed?
(Multiple Choice)
4.9/5  (40)
(40)
Equilibrium: A uniform 300-kg beam, 6.00 m long, is freely pivoted at P, as shown in the figure. The beam is supported in a horizontal position by a light strut, 5.00 m long, which is freely pivoted at Q and is loosely pinned to the beam at R. A load of mass is suspended from the end of the beam at S. A maximum compression of 23,000 N in the strut is permitted, due to safety. The maximum mass M of the load is closest to 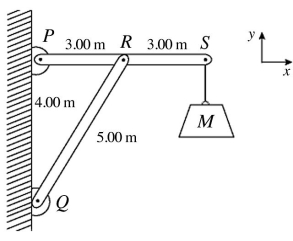
(Multiple Choice)
4.7/5  (34)
(34)
Rotational dynamics about a fixed axis: A very thin horizontal, 2.00-m long, 5.00-kg uniform beam that lies along the east-west direction is acted on by two forces. At the east end of the beam, a 200-N force pushes downward. At the west end of the beam, a 200-N force pushes upward. What is the angular acceleration of the beam?
(Multiple Choice)
4.7/5  (38)
(38)
Rotational kinematics: The angular velocity of a 755-g wheel 15.0 cm in diameter is given by the equation ω(t) = (2.00 rad/s2)t + (1.00 rad/s4)t3.
(a) Through how many radians does the wheel turn during the first 2.00 s of its motion?
(b) What is the angular acceleration (in rad/s2) of the wheel at the end of the first 2.00 s of its motion?
(Essay)
4.9/5  (34)
(34)
Equilibrium: A uniform sign is supported against a wall at point P as shown in the figure. If the sign is a square 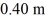 on a side and its mass is
on a side and its mass is 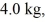 what is the magnitude of the horizontal force that the wall at P experiences?
what is the magnitude of the horizontal force that the wall at P experiences? 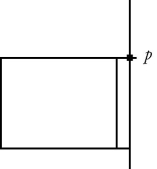
(Multiple Choice)
4.8/5  (44)
(44)
Equilibrium: In the figure, the horizontal lower arm has a mass of 2.8 kg and its center of gravity is 12 cm from the elbow joint pivot. How much force FM must the vertical extensor muscle in the upper arm exert on the lower arm to hold a 7.5 kg shot put? 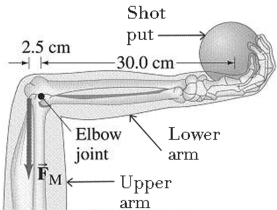
(Multiple Choice)
4.9/5  (40)
(40)
Showing 21 - 40 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)