Exam 8: Momentum, Impulse, and Collisions
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Rotational kinetic energy: A futuristic design for a car is to have a large solid disk-shaped flywheel within the car storing kinetic energy. The uniform flywheel has mass 370 kg with a radius of 0.500 m and can rotate up to 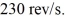 Assuming all of this stored kinetic energy could be transferred to the linear velocity of the
Assuming all of this stored kinetic energy could be transferred to the linear velocity of the 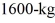 car, find the maximum attainable speed of the car.
car, find the maximum attainable speed of the car.
(Short Answer)
4.7/5  (37)
(37)
Equilibrium: A nonuniform, 80.0-g, meterstick balances when the support is placed at the 51.0-cm mark. At what location on the meterstick should a 5.00-g tack be placed so that the stick will balance at the 50.0 cm mark?
(Multiple Choice)
4.7/5  (43)
(43)
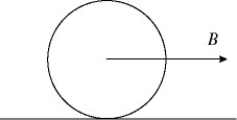
Rotational dynamics about a moving axis: A lawn roller in the form of a uniform solid cylinder is being pulled horizontally by a horizontal force B applied to an axle through the center of the roller, as shown in the figure. The roller has radius 0.65 meters and mass 51 kg and rolls without slipping. What magnitude of the force B is required to give the center of mass of the roller an acceleration of 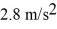 ?
? 
(Short Answer)
4.9/5  (35)
(35)
Basic rotational quantities: As you are leaving a building, the door opens outward. If the hinges on the door are on your right, what is the direction of the angular velocity of the door as you open it?
(Multiple Choice)
4.8/5  (28)
(28)
Rotational dynamics about a fixed axis: A wheel has a radius of 0.40 m and is mounted on frictionless bearings. A block is suspended from a rope that is wound on the wheel and attached to it (see figure). The wheel is released from rest and the block descends 1.5 m in 2.00 s without any slipping of the rope. The tension in the rope during the descent of the block is 20 N. What is the moment of inertia of the wheel? 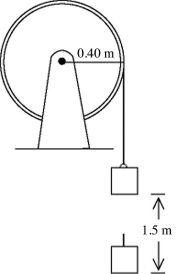
(Multiple Choice)
4.9/5  (40)
(40)
Equilibrium: A stepladder consists of two halves, hinged at the top, and connected by a tie rod that keeps the two halves from spreading apart. In this particular instance, the two halves are 2.50 m long, the tie rod is connected to the center of each half and is 70.0 cm long. An 800-N person stands 3/5 of the way up the stepladder, as shown in the figure. Neglecting the weight of the ladder, and assuming that the ladder is resting on a smooth floor, what is the tension in the tie rod? Note: To solve this problem you must "cut" the ladder in half and consider the equilibrium of forces and torques acting on each half of the ladder. 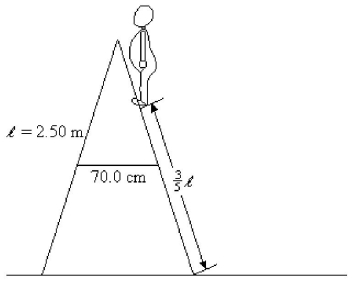
(Multiple Choice)
4.8/5  (44)
(44)
Rotational dynamics about a fixed axis: A very thin uniform rod, 2.40 m long and of weight 135 N, has a frictionless hinge at its lower end. It starts out vertically from rest and falls, pivoting about the hinge. Just as it has rotated through an angle of 55.0°, what is the downward acceleration of the end farthest from the hinge?
(Multiple Choice)
4.7/5  (32)
(32)
Equilibrium: A 5.0-m long, 12-kg uniform ladder rests against a smooth vertical wall with the bottom of the ladder 3.0 m from the wall. The coefficient of static friction between the floor and the ladder is 0.28. What distance, measured along the ladder from the bottom, can a 60-kg person climb before the ladder starts to slip?
(Multiple Choice)
4.8/5  (36)
(36)
Rolling: A uniform solid sphere of mass 1.5 kg and diameter 30.0 cm starts from rest and rolls without slipping down a 35° incline that is 7.0 m long.
(a) Calculate the linear speed of the center of the sphere when it reaches the bottom of the incline.
(b) Determine the angular speed of the sphere about its center at the bottom of the incline.
(c) Through what angle (in radians) does this sphere turn as it rolls down the incline?
(d) Does the linear speed in (a) depend on the radius or mass of the sphere? Does the angular speed in (b) depend on the radius or mass of the sphere?
(Essay)
4.8/5  (41)
(41)
Equilibrium: A 20.0-kg uniform plank is supported by the floor at one end and by a vertical rope at the other as shown in the figure. A 50.0-kg mass person stands on the plank a distance three-fourths of the length plank from the end on the floor. 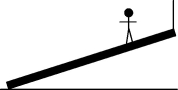 (a) What is the tension in the rope?
(b) What is the magnitude of the force that the floor exerts on the plank?
(a) What is the tension in the rope?
(b) What is the magnitude of the force that the floor exerts on the plank?
(Essay)
4.7/5  (46)
(46)
Rotational kinematics: The angular acceleration of a wheel is given in 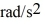 by
by 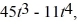 where t is in seconds. If the wheel starts from rest at
where t is in seconds. If the wheel starts from rest at 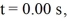 when is the next time the wheel is at rest?
when is the next time the wheel is at rest?
(Multiple Choice)
4.8/5  (32)
(32)
Rotational kinematics: A turbine blade rotates with angular velocity ω(t) = 2.00 rad/s- 2.1.00 rad/s3 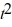 . What is the angular acceleration of the blade at
. What is the angular acceleration of the blade at 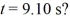
(Multiple Choice)
4.9/5  (36)
(36)
Equilibrium: A 30.0-kg child sits on one end of a long uniform beam having a mass of 20.0 kg, and a 40.0-kg child sits on the other end. The beam balances when a fulcrum is placed below the beam a distance 1.10 m from the 30.0-kg child. How long is the beam?
(Multiple Choice)
4.9/5  (39)
(39)
Equilibrium: In the figure, a uniform ladder 12 meters long rests against a vertical frictionless wall. The ladder weighs 400 N and makes an angle θ of 79° with the floor. A man weighing 790 N climbs slowly up the ladder When he has climbed to a point that is 7.8 m from the base of the ladder, the ladder starts to slip. What is the coefficient of static friction between the floor and the ladder? 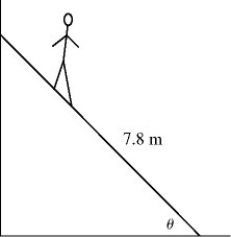
(Short Answer)
4.9/5  (46)
(46)
Moment of inertia: A uniform solid sphere has a moment of inertia I about an axis tangent to its surface. What is the moment of inertia of this sphere about an axis through its center?
(Multiple Choice)
4.8/5  (30)
(30)
Precession: A bicycle wheel of radius 0.36 m and mass 3.2 kg is set spinning at 4.00 rev/s. A very light bolt is attached to extend the axle in length, and a string is attached to the axle at a distance of 0.10 m from the wheel. Initially the axle of the spinning wheel is horizontal, and the wheel is suspended only from the string. We can ignore the mass of the axle and spokes. At what rate will the wheel process about the vertical?
(Multiple Choice)
5.0/5  (40)
(40)
Equilibrium: A 20.0-kg uniform door has a width of 1.20 m and a height of 2.50 m. The door is mounted on a post by a pair of hinges, marked 1 and 2 in the figure, at the top and bottom of the door. An external force of 60.0 N, at an angle of 30.0° above the horizontal, is applied to the small doorknob, as shown in the figure. The doorknob is 1.00 m above the bottom of the door.
(a) Find the x component of the force that hinge 1 exerts on the door at the top.
(b) Find the SUM of the y components of the forces that hinges 1 and 2 together exert on the door. 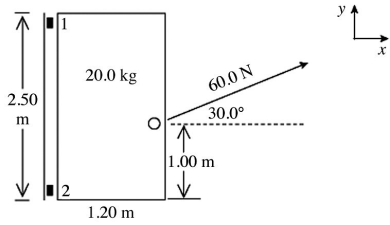
(Essay)
4.9/5  (36)
(36)
Torque: A 1.10-kg wrench is acting on a nut trying to turn it. The length of the wrench lies directly to the east of the nut. A force 150.0 N acts on the wrench at a position 15.0 cm from the center of the nut in a direction 30.0° north of east. What is the magnitude of the torque about the center of the nut?
(Multiple Choice)
4.8/5  (28)
(28)
Angular momentum: A 500-g particle is located at the point 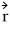 = 4m
= 4m  + 3m
+ 3m  - 2m
- 2m  and is moving with a velocity
and is moving with a velocity 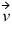 = 5 m/s
= 5 m/s  - 2m/s
- 2m/s  + 4 m/s
+ 4 m/s  . What is the angular momentum of this particle about the origin?
. What is the angular momentum of this particle about the origin?
(Multiple Choice)
4.9/5  (28)
(28)
Showing 81 - 99 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)