Exam 8: Momentum, Impulse, and Collisions
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Rotational dynamics about a moving axis: If an irregularly shaped object (such as a wrench) is dropped from rest in a classroom and feels no air resistance, it will
(Multiple Choice)
4.9/5  (43)
(43)
Equilibrium: A heavy boy and a lightweight girl are balanced on a massless seesaw. If they both move forward so that they are one-half their original distance from the pivot point, what will happen to the seesaw? Assume that both people are small enough compared to the length of the seesaw to be thought of as point masses.
(Multiple Choice)
4.9/5  (32)
(32)
Rotational kinetic energy: At any angular speed, a certain uniform solid sphere of diameter D has half as much rotational kinetic energy as a certain uniform thin-walled hollow sphere of the same diameter when both are spinning about an axis through their centers. If the mass of the solid sphere is M, the mass of the hollow sphere is
(Multiple Choice)
4.8/5  (39)
(39)
Rotational dynamics about a fixed axis: The two rotating systems shown in the figure differ only in that the two identical movable masses are positioned at different distances from the axis of rotation. If you release the hanging blocks simultaneously from rest, and if the ropes do not slip, which block lands first? 
(Multiple Choice)
4.9/5  (29)
(29)
Moment of inertia: In the figure, a weightlifter's barbell consists of two identical uniform spherical masses each with radius 0.17 m and mass of 50 kg. The weights are connected by a 0.96-m uniform steel rod with a mass of 12 kg. Find the moment of inertia of the barbell about the axis through the center (see figure). 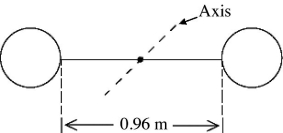
(Short Answer)
4.8/5  (38)
(38)
Basic rotational quantities: When a rigid body rotates about a fixed axis, all the points in the body have the same
(Multiple Choice)
4.9/5  (46)
(46)
Conservation of angular momentum: A record is dropped vertically onto a freely rotating (undriven) turntable. Frictional forces act to bring the record and turntable to a common angular speed. If the rotational inertia of the record is 0.54 times that of the turntable, what percentage of the initial kinetic energy is lost?
(Multiple Choice)
4.9/5  (41)
(41)
Torque: A light triangular plate OAB is in a horizontal plane. Three forces, 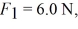
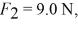 and
and 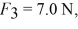 act on the plate, which is pivoted about a vertical axes through point O. In the figure,
act on the plate, which is pivoted about a vertical axes through point O. In the figure, 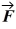 2 is perpendicular to OB. Consider the counterclockwise sense as positive. The sum of the torques about the vertical axis through point O, acting on the plate due to forces F1, F2, and F3, is closest to
2 is perpendicular to OB. Consider the counterclockwise sense as positive. The sum of the torques about the vertical axis through point O, acting on the plate due to forces F1, F2, and F3, is closest to 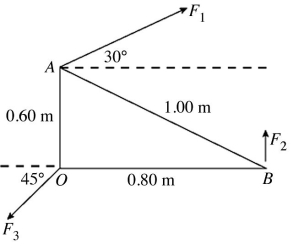
(Multiple Choice)
4.8/5  (43)
(43)
Rotational kinematics with constant angular acceleration: A machinist turns the power on to a grinding wheel, which is at rest at time t = 0.00 s. The wheel accelerates uniformly for 10 s and reaches the operating angular velocity of 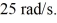 The wheel is run at that angular velocity for 37 s and then power is shut off. The wheel decelerates uniformly at
The wheel is run at that angular velocity for 37 s and then power is shut off. The wheel decelerates uniformly at 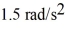 until the wheel stops. In this situation, the time interval of angular deceleration (slowing down) is closest to:
until the wheel stops. In this situation, the time interval of angular deceleration (slowing down) is closest to:
(Multiple Choice)
4.9/5  (39)
(39)
Rolling: A uniform solid 5.25-kg cylinder is released from rest and rolls without slipping down an inclined plane inclined at 18° to the horizontal. How fast is it moving after it has rolled 2.2 m down the plane?
(Multiple Choice)
4.9/5  (35)
(35)
Rotational kinematics with constant angular acceleration: When a 2.75-kg fan, having blades 18.5 cm long, is turned off, its angular speed decreases uniformly from 10.0 rad/s to 6.30 rad/s in 5.00 s.
(a) What is the magnitude of the angular acceleration of the fan?
(b) Through what angle (in degrees) does it turn while it is slowing down during the 5.00 s?
(c) If its angular acceleration does not change, how long after it is turned off does it take the fan to stop.
(Essay)
4.8/5  (35)
(35)
Rotational kinematics with constant angular acceleration: A 3.45-kg centrifuge takes 100 s to spin up from rest to its final angular speed with constant angular acceleration. A point located 8.00 cm from the axis of rotation of the centrifuge moves with a speed of 150 m/s when the centrifuge is at full speed.
(a) What is the angular acceleration (in rad/s2) of the centrifuge as it spins up?
(b) How many revolutions does the centrifuge make as it goes from rest to its final angular speed?
(Essay)
4.8/5  (42)
(42)
Rotational dynamics about a fixed axis: A torque of 12 N ∙ m is applied to a solid, uniform disk of radius 0.50 m, causing the disk to accelerate at 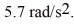 What is the mass of the disk?
What is the mass of the disk?
(Multiple Choice)
4.9/5  (41)
(41)
Conservation of angular momentum: A turntable has a radius of 0.80 m and a moment of inertia of 2.0 kg · m2. The turntable is rotating with an angular velocity of 1.5 rad/s about a vertical axis though its center on frictionless bearings. A very small 0.40-kg ball is projected horizontally toward the turntable axis with a velocity of 3.0 m/s. The ball is caught by a very small and very light cup-shaped mechanism on the rim of the turntable (see figure). The percent of the initial kinetic energy of the system that is lost during the capture of the ball is closest to 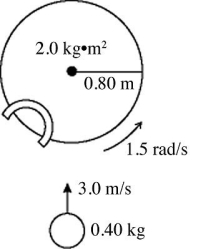
(Multiple Choice)
4.9/5  (39)
(39)
Equilibrium: Two identical ladders are 3.0 m long and weigh 600 N each. They are connected by a hinge at the top and are held together by a horizontal rope, 1.0 m above the smooth floor forming a symmetric "A" arrangement. The angle between the ladders is 60° and both ladders have their center of gravity at their midpoint. What is the tension in the rope?
(Multiple Choice)
4.8/5  (31)
(31)
Rolling: A solid, uniform sphere of mass 2.0 kg and radius 1.7 m rolls from rest without slipping down an inclined plane of height 7.0 m. What is the angular velocity of the sphere at the bottom of the inclined plane?
(Multiple Choice)
4.9/5  (46)
(46)
Rotational kinematics with constant angular acceleration: A 1.25-kg ball begins rolling from rest with constant angular acceleration down a hill. If it takes 3.60 s for it to make the first complete revolution, how long will it take to make the next complete revolution?
(Short Answer)
4.8/5  (35)
(35)
Rotational kinetic energy: An extremely light rod 1.00 m long has a 2.00-kg mass attached to one end and a 3.00-kg mass attached to the other. The system rotates at a constant angular speed about a fixed axis perpendicular to the rod that passes through the rod 30.0 cm from the end with the 3.00-kg mass attached. The kinetic energy of the system is measured to be 100.0 J.
(a) What is the moment of inertia of this system about the fixed axis?
(b) What is the angular speed (in revolutions per second) of this system?
(Essay)
4.8/5  (31)
(31)
Equilibrium: A dump truck has a large cubical concrete block in its bed. The coefficients of friction between this block and the floor of the bed are µk = 0.450 and µs = 0.650. As the bed is slowly tilted above the horizontal, will the brick first begin to slide or will it first tip over?
(Multiple Choice)
4.8/5  (37)
(37)
Showing 41 - 60 of 99
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)