Exam 11: Equilibrium and Elasticity
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Simple pendulum: A frictionless pendulum released from 65 degrees with the vertical will vibrate with the same frequency as if it were released from 5 degrees with the vertical because the period is independent of the amplitude and mass.
(True/False)
4.8/5  (44)
(44)
Simple harmonic motion: A sewing machine needle moves up and down in simple harmonic motion with an amplitude of 1.27 cm and a frequency of 2.55 Hz.
(a) What is the maximum speed of the needle?
(b) What is the maximum acceleration of the needle?
(Essay)
4.8/5  (33)
(33)
Damped harmonic motion: An ideal massless spring with a spring constant of 2.00 N/m is attached to an object of 75.0 g. The system has a small amount of damping. If the amplitude of the oscillations decreases from 10.0 mm to 5.00 mm in 15.0 s, what is the magnitude of the damping constant b?
(Multiple Choice)
5.0/5  (40)
(40)
Simple harmonic motion: The position of an object that is oscillating on an ideal spring is given by the equation x = (12.3 cm) cos[(1.26s-1)t]. At time t = 0.815 s,
(a) how fast is the object moving?
(b) what is the magnitude of the acceleration of the object?
(Essay)
4.9/5  (32)
(32)
Energy in SHM: A 1.5-kg mass attached to an ideal massless spring with a spring constant of 20.0 N/m oscillates on a horizontal, frictionless track. At time t = 0.00 s, the mass is released from rest at x = 10.0 cm. (That is, the spring is stretched by 10.0 cm.)
(a) Find the frequency of the oscillations.
(b) Determine the maximum speed of the mass. At what point in the motion does the maximum speed occur?
(c) What is the maximum acceleration of the mass? At what point in the motion does the maximum acceleration occur?
(d) Determine the total energy of the oscillating system.
(e) Express the displacement x as a function of time t.
(Essay)
4.7/5  (40)
(40)
Energy in SHM: If we double only the amplitude of a vibrating ideal mass-and-spring system, the mechanical energy of the system
(Multiple Choice)
4.9/5  (42)
(42)
Simple harmonic motion: Which of following graphs describes simple periodic motion with amplitude 2.00 cm and angular frequency 2.00 rad/s?
(Multiple Choice)
4.7/5  (39)
(39)
Mass on a spring: In the figure, two masses, M = 16 kg and m = 12.8 kg, are connected to a very light rigid bar and are attached to an ideal massless spring of spring constant 100 N/m. The system is set into oscillation with an amplitude of 78 cm. At the instant when the acceleration is at its maximum, the 16-kg mass separates from the 12.8-kg mass, which then remains attached to the spring and continues to oscillate. What will be the amplitude of oscillation of the 12.8-kg mass? 
(Multiple Choice)
4.8/5  (38)
(38)
Mass on a spring: A mass M is attached to an ideal massless spring. When this system is set in motion with amplitude A, it has a period T. What is the period if the amplitude of the motion is increased to 2A?
(Multiple Choice)
5.0/5  (37)
(37)
Energy in SHM: A 0.025-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 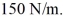 The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is
The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is 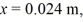 what is the kinetic energy of the block?
what is the kinetic energy of the block?
(Multiple Choice)
4.8/5  (33)
(33)
Mass on a spring: A mass M is attached to an ideal massless spring. When this system is set in motion, it has a period T. What is the period if the mass is doubled to 2M?
(Multiple Choice)
4.9/5  (50)
(50)
Resonance: In designing buildings to be erected in an area prone to earthquakes, what relationship should the designer try to achieve between the natural frequency of the building and the typical earthquake frequencies?
(Multiple Choice)
4.8/5  (34)
(34)
Resonance: An object of mass of 2.0 kg hangs from an ideal massless spring with a spring constant of 50 N/m. An oscillating force F = (4.8 N) cos[(3.0 rad/s)t] is applied to the object. What is the amplitude of the resulting oscillations? You can neglect damping.
(Multiple Choice)
4.9/5  (37)
(37)
Energy in SHM: An object is attached to a vertical ideal massless spring and bobs up and down between the two extreme points A and B. When the kinetic energy of the object is a minimum, the object is located
(Multiple Choice)
4.9/5  (34)
(34)
Energy in SHM: In simple harmonic motion, the speed is greatest at that point in the cycle when
(Multiple Choice)
4.8/5  (28)
(28)
Simple harmonic motion: The simple harmonic motion of an object is described by the graph shown in the figure. What is the equation for the position x(t) of the object as a function of time t? 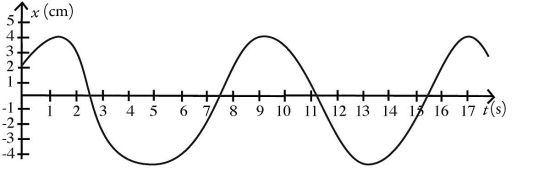
(Multiple Choice)
4.8/5  (35)
(35)
Damped harmonic motion: A 25 kg object is undergoing lightly damped harmonic oscillations. If the maximum displacement of the object from its equilibrium point drops to 1/3 its original value in 1.8 s, what is the value of the damping constant b?
(Multiple Choice)
4.8/5  (40)
(40)
Damped harmonic motion: A 5.0-kg block is attached to an ideal massless spring whose spring constant is 125 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a position at x = +0.687 m and is released from rest. The block then executes lightly damped oscillation along the x-axis, and the damping force is proportional to the velocity. When the block first returns to x = 0.00 m, its x component of velocity is -2.0 m/s and its x component of acceleration is +5.6 m/s2.
(a) What is the magnitude of the acceleration of the block upon release at x = +0.687 m.
(b) Find the damping constant b.
(Essay)
4.7/5  (31)
(31)
Energy in SHM: A 0.50-kg object is attached to an ideal massless spring of spring constant 20 N/m along a horizontal, frictionless surface. The object oscillates in simple harmonic motion and has a speed of 1.5 m/s at the equilibrium position.
(a) What is the amplitude of vibration?
(b) At what location are the kinetic energy and the potential energy of the system the same?
(Essay)
4.9/5  (35)
(35)
Mass on a spring: A 56.0 kg bungee jumper jumps off a bridge and undergoes simple harmonic motion. If the period of oscillation is 11.2 s, what is the spring constant of the bungee cord, assuming it has negligible mass compared to that of the jumper?
(Multiple Choice)
4.8/5  (31)
(31)
Showing 21 - 40 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)