Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
Trish attends an aerobics class four times each week. She would like to estimate the mean number of minutes of continuous exercise until her heart reaches 90 beats per minute. If it can be assumed that 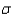 = 1.7 minutes, how large a sample is needed so that it will be possible to assert with 99% confidence that the sample mean has a margin of error of at most 0.62 minutes?
______________
= 1.7 minutes, how large a sample is needed so that it will be possible to assert with 99% confidence that the sample mean has a margin of error of at most 0.62 minutes?
______________
(Short Answer)
4.9/5  (37)
(37)
A term confidence level refers to an estimate of a population parameter, expressed as a range of values within which the unknown but true parameter presumably lies.
(True/False)
4.9/5  (34)
(34)
A simple extension of the estimation of a binomial proportion p is the estimation of the difference between two binomial proportions 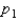 and
and 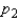 .
.
(True/False)
4.9/5  (31)
(31)
A point estimate of a population parameter will likely be different from the corresponding population value due to the fact that point estimates are subject to sampling error.
(True/False)
4.8/5  (34)
(34)
A random sample of 60 people revealed it took an average of 55 minutes with a standard deviation of 10 minutes for a person to complete a loan application at the bank. Construct a 90% confidence interval for 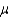 , the true time it takes any person to complete the loan form.
______________
, the true time it takes any person to complete the loan form.
______________
(Short Answer)
4.9/5  (36)
(36)
If you wish to estimate the difference between two population means when the population variances are known, the 99% confidence interval estimate can be developed using which of the following critical values of z?
(Multiple Choice)
4.7/5  (44)
(44)
In constructing a 95% confidence interval estimate for the difference between the means of two normally distributed populations, where the unknown population variances are assumed not to be equal, summary statistics computed from two independent samples are: 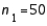 ,
, 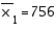 ,
, 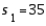 ,
, 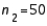 ,
, 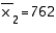 , and
, and 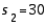 . The upper confidence limit is:
. The upper confidence limit is:
(Multiple Choice)
4.9/5  (37)
(37)
A questionnaire is designed to investigate attitudes about political corruption in government. The experimenter would like to survey two different groups--Republicans and Democrats--and compare the responses to various "yes-no" questions for the two groups. The experimenter requires that the sampling error for the difference in the proportion of yes responses for the two groups is no more than 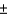 4 percentage points with probability equal to 0.95. If the two samples are both the same size, how large should the samples be?
______________
4 percentage points with probability equal to 0.95. If the two samples are both the same size, how large should the samples be?
______________
(Short Answer)
4.9/5  (40)
(40)
A 95% lower confidence bound (LCB) for the difference between population proportions can be constructed using the following equation:
LCB = 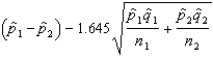
(True/False)
4.9/5  (36)
(36)
An unbiased estimator of a population parameter is an estimator whose variance is the same as the actual value of the population variance.
(True/False)
4.9/5  (37)
(37)
A sample statistic such that the mean of all its possible values equals the population parameter the statistic seeks to estimate is an unbiased estimator.
(True/False)
4.7/5  (25)
(25)
Assume that two independent random samples of sizes 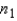 and
and 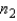 have been selected from binomial populations with parameters
have been selected from binomial populations with parameters 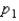 and
and 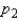 , respectively. The standard error of the sampling distribution of
, respectively. The standard error of the sampling distribution of 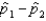 , the difference between sample proportions, is estimated by
, the difference between sample proportions, is estimated by 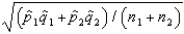 .
.
(True/False)
4.8/5  (35)
(35)
A random sample of 80 jars of grape jelly has a mean weight of 20 oz. with a standard deviation of 1.7 oz. Construct a 99% confidence interval for 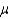 , the true weight of a jar of jelly.
______________
, the true weight of a jar of jelly.
______________
(Short Answer)
4.7/5  (35)
(35)
A comparison between the average jail time of bank robbers and car thieves yielded the following results (in years): 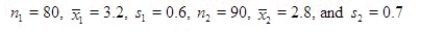 Estimate (
Estimate ( 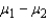 ), the difference in mean years of jail time.
______________
Find the margin of error for your estimate.
______________
), the difference in mean years of jail time.
______________
Find the margin of error for your estimate.
______________
(Short Answer)
4.7/5  (35)
(35)
The Postmaster at the Harrington Post Office would like to compare the delivery times to two different locations which are the same number of miles from Harrington. A random sample of letters are to be divided into two equal groups, the first delivered to Location A and the second delivered to Location B. Each letter will be delivered on a randomly selected day and the number of days for each letter to arrive at its destination is recorded. The measurements for both groups are expected to have a range (variability) of approximately 4 days. If the estimate of the difference in mean delivery times is desired to be correct to within 1 day with probability equal to 0.99, how many letters must be included in each group? Assume n1 = n2 = n.
______________
(Short Answer)
4.9/5  (38)
(38)
Suppose you wish to estimate a population mean based on a random sample of n observations, and prior experience suggests that 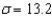 . If you wish to estimate
. If you wish to estimate 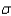 correct to within 1.8, with probability equal to 0.95, how many observations should be included in your sample?
______________
correct to within 1.8, with probability equal to 0.95, how many observations should be included in your sample?
______________
(Short Answer)
4.8/5  (39)
(39)
A random sample of 45 door-to-door encyclopedia salespersons were asked how long on average they were able to talk to the potential customer. Their answers revealed a mean of 8.5 minutes with a variance of 9 minutes. Construct a 95% confidence interval for 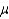 , the time it takes an encyclopedia salesperson to talk to a potential customer.
______________
, the time it takes an encyclopedia salesperson to talk to a potential customer.
______________
(Short Answer)
4.8/5  (35)
(35)
The difference between two sample means 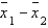 is an unbiased estimator of the difference between two population means
is an unbiased estimator of the difference between two population means 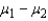 .
.
(True/False)
4.9/5  (33)
(33)
A sample statistic such that the mean of all its possible values differs from the population parameter the statistics seeks to estimate is called:
(Multiple Choice)
4.7/5  (32)
(32)
Showing 101 - 120 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)