Exam 8: Large-Sample Estimation
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
The sample size needed to estimate a population mean within 1.5 units with a 95% confidence when the population standard deviation equals 10 is:
(Multiple Choice)
4.9/5  (37)
(37)
A point estimate is a single number that is used as an estimate of a population parameter or population characteristic. It is usually derived from a random sample from the population of interest.
(True/False)
4.9/5  (36)
(36)
A laboratory technician is interested in the proportion of 1-liter containers used in the lab that are glass. How many containers should be sampled in order to estimate this proportion with a margin of error of less than 0.2 with 99% confidence?
______________
(Short Answer)
4.9/5  (32)
(32)
After constructing a confidence interval estimate for a population mean, you believe that the interval is useless because it is too wide. In order to correct this problem, you need to:
(Multiple Choice)
4.8/5  (41)
(41)
If the population deviation 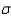 is known and we wish to estimate the population mean
is known and we wish to estimate the population mean 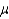 with 90% confidence, what is the appropriate critical value z to use?
with 90% confidence, what is the appropriate critical value z to use?
(Multiple Choice)
4.8/5  (43)
(43)
Assume that the population standard deviation of annual incomes of all Michigan residents is $2,500. How many individuals must we include in a simple random sample if we want to be 95% confident that the population mean incomes lies within $150 of our sample mean income?
______________
(Short Answer)
4.9/5  (32)
(32)
Two independent random samples of sizes  and
and 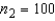 have been selected from binomial populations with parameters
have been selected from binomial populations with parameters 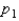 and
and 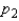 , respectively, and resulted in 38 and 65 success, respectively. Then, the point estimation of the difference
, respectively, and resulted in 38 and 65 success, respectively. Then, the point estimation of the difference 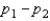 is -27.
is -27.
(True/False)
4.7/5  (42)
(42)
The meat department of a local supermarket packages ground beef using meat trays of two sizes: one designed to hold approximately 1.5 pounds of meat, and one that holds approximately 3 pounds. A random sample of 36 packages in the smaller meat trays produced weight measurements with an average of 1.51 pounds and a standard deviation of 0.20 pound.
Construct a 99% confidence interval for the average weight of all packages sold in the small meat trays by this supermarket chain.
______________
What does the phrase "99% confident" mean?
________________________________________________________
Suppose that the quality control department of this supermarket chain intends that the amount of ground beef in the smaller trays should be 1.5 pound on average. Should the confidence interval in part (a) concern the quality control department?
______________
Explain.
________________________________________________________
(Essay)
4.8/5  (34)
(34)
A 99% confidence interval estimate for a population mean 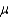 is determined to be 85.58 to 96.62. If the confidence level is reduced to 90%, the confidence interval for
is determined to be 85.58 to 96.62. If the confidence level is reduced to 90%, the confidence interval for 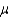 :
:
(Multiple Choice)
4.8/5  (31)
(31)
The z-value needed to construct a 92.5% confidence interval estimate for the difference between two population proportions is:
(Multiple Choice)
4.9/5  (37)
(37)
The margin of error equals the sum of an estimator's squared bias plus its variance.
(True/False)
4.8/5  (41)
(41)
A 99% upper confidence bound (UCB) for the difference between population means in case of large samples (both 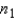 and
and 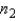 greater than 30) can be constructed using the following equation:
UCB =
greater than 30) can be constructed using the following equation:
UCB = 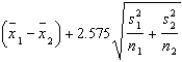
(True/False)
4.8/5  (28)
(28)
A confidence interval for the population mean 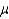 will contain the true value of
will contain the true value of 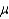 as long as the point estimate
as long as the point estimate 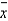 is within the lower and the upper confidence limits.
is within the lower and the upper confidence limits.
(True/False)
4.8/5  (34)
(34)
Which of the following statements is true with respect to a point estimate?
(Multiple Choice)
4.8/5  (30)
(30)
In estimating the difference between two population means, if a 90% confidence interval estimate includes zero, then we can conclude that there is a 90% chance that the difference between the two population means is zero.
(True/False)
4.9/5  (35)
(35)
The lower limit of the 90% confidence interval for the population proportion p, given that n = 400; and 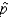 = 0.10, is 0.1247.
= 0.10, is 0.1247.
(True/False)
4.7/5  (30)
(30)
The z-value needed to construct a 97.8% confidence interval estimate for the difference between two population proportions is:
(Multiple Choice)
4.7/5  (34)
(34)
An estimator is unbiased if the mean of its sampling distribution is the population parameter being estimated.
(True/False)
4.7/5  (39)
(39)
The standard error of the sampling distribution of 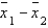 is given by the formula:
SE =
is given by the formula:
SE = 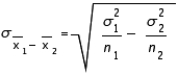 .
.
(True/False)
4.9/5  (45)
(45)
The best estimator of the difference between two population means 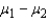 is the difference between two sample means
is the difference between two sample means 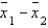 .
.
(True/False)
4.9/5  (31)
(31)
Showing 141 - 160 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)