Exam 15: Vector Fields
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the area of the surface over the given region. Use a computer algebra system to verify your results. The sphere,
(Multiple Choice)
4.9/5  (28)
(28)
Find the flux of over the closed surface let be the outward unit normal vector of the surface).
cube bounded by
(Multiple Choice)
4.9/5  (42)
(42)
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field . Find , where is the upper surface of the cylindrical container.
(Multiple Choice)
4.8/5  (41)
(41)
A stone weighing 2 pounds is attached to the end of a four-foot string and is whirled horizontally with one end held fixed. It makes 1 revolution per second. Find the work done by the Force F that keeps the stone moving in a circular path. [Hint: Use Force = (mass)(centripetal Acceleration).] Round your answer to two decimal places, if required.
(Multiple Choice)
4.9/5  (43)
(43)
Verify Green's Theorem by evaluating both integrals for the path defined as the boundary of the region lying between the graphs of and .
(Multiple Choice)
4.9/5  (36)
(36)
and .
Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (44)
(44)
Find the value of the line integral
(Hint: If is conservative, the integration may be easier on an alternate path.)
(Multiple Choice)
4.9/5  (35)
(35)
(Hint: If is conservative, the integration may be easier on an alternate path.)
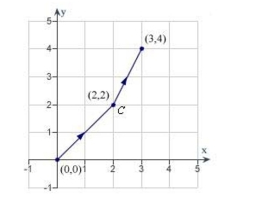
(Multiple Choice)
5.0/5  (34)
(34)
plane and the coordinates planes. Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral.
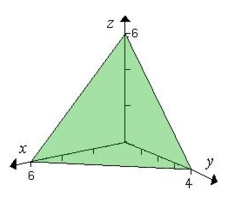
(Multiple Choice)
4.9/5  (39)
(39)
(Hint: If is conservative, the integration may be easier on an alternate path.)
(Multiple Choice)
4.9/5  (45)
(45)
Find the flux of through , , where is the upward unit normal vector to S.
, first octant
(Multiple Choice)
4.8/5  (41)
(41)
Evaluate the line integral Theorem of Line Integrals, where is the line segment from to .
(Multiple Choice)
4.9/5  (41)
(41)
The surface of the dome on a new museum is given by , where and and is in meters. Find the surface area of the dome.
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)