Exam 15: Vector Fields
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral.
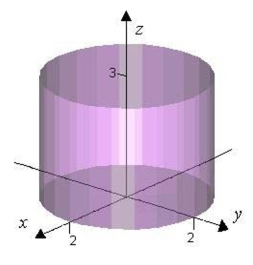
(Multiple Choice)
4.7/5  (40)
(40)
and and the coordinate planes. Verify the Divergence Theorem by evaluating as a surface integral and as a triple integral. Round your answer to two decimal places wherever applicable.
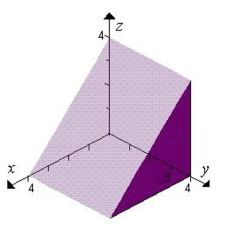
(Multiple Choice)
4.8/5  (44)
(44)
Use Stokes's Theorem to evaluate and is the first-octant portion of over
Use a computer algebra system to verify your result.
(Multiple Choice)
4.7/5  (44)
(44)
Find an equation of the tangent plane to the surface represented by the vector-valued function at the given point.
(Multiple Choice)
4.8/5  (36)
(36)
Find the value of the line integral , where and
(Hint: If is conservative, the integration may be easier on an alternate path.)
(Multiple Choice)
4.8/5  (39)
(39)
Use the Divergence Theorem to evaluate Verify your answer by evaluating the integral as a triple integral.
: cube bounded by the planes
(Multiple Choice)
4.9/5  (39)
(39)
Find the gradient vector for the scalar function. (That is, find the conservative vector field for the potential function.)
(Multiple Choice)
4.9/5  (36)
(36)
Green's Theorem to evaluate the integral
for the path : boundary of the region lying between the graphs of and .
(Multiple Choice)
4.8/5  (40)
(40)
Find the value of the line integral on the closed path consisting of line segments from to , from to , and then from to , where .
(Hint: If is conservative, the integration may be easier on an alternate path.)
(Multiple Choice)
4.9/5  (36)
(36)
Write a set of parametric equations for the surface of revolution obtained by revolving the graph of the function about the -axis.
(Multiple Choice)
4.8/5  (37)
(37)
Use a computer algebra system and the result "The area of a plane region bounded by the simple closed path given in polar coordinates is to find the area of the region bounded by the graphs of the polar equation . Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (44)
(44)
Use Green's Theorem to evaluate the line integral where is the boundary of the region lying between the graphs of the circle and the ellipse .
(Multiple Choice)
4.8/5  (31)
(31)
Use a computer algebra system to evaluate where is , . Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (36)
(36)
Showing 61 - 80 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)