Exam 15: Vector Fields
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Evaluate the line integral using the Fundamental Theorem of Line Integrals. Use a computer algebra system to verify your results. : circle clockwise from to
(Multiple Choice)
4.7/5  (38)
(38)
Find the rectangular equation for the surface by eliminating the parameters from the vector-valued function .
(Multiple Choice)
4.7/5  (33)
(33)
Calculate the line integral along starting at the point and ending at .
(Multiple Choice)
4.9/5  (33)
(33)
Evaluate the integral along the path , defined as -axis from to .
(Multiple Choice)
4.9/5  (33)
(33)
Find the gradient vector for the scalar function. (That is, find the conservative vector field for the potential function.)
(Multiple Choice)
4.9/5  (40)
(40)
Use Green's Theorem to evaluate the integral path defined as .
(Multiple Choice)
4.7/5  (37)
(37)
Find the value of the line integral . (Hint: If is conservative, the integration may be easier on an alternate path.)
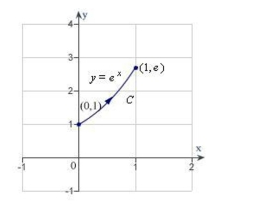
(Multiple Choice)
4.9/5  (44)
(44)
Match the following vector -valued function with its graph.
(Multiple Choice)
4.8/5  (30)
(30)
Use Stokes's Theorem to evaluate where and is the first-octant portion of over . Use a computer algebra system to verify your result.
(Multiple Choice)
4.8/5  (35)
(35)
Use a computer algebra system and the result "The centroid of the region having area bounded by the simple closed path is to find the centroid of the region bounded by the graphs of and .
(Multiple Choice)
4.7/5  (38)
(38)
Find the maximum value of in the xy-plane, oriented counterclockwise.
(Multiple Choice)
4.9/5  (29)
(29)
and is .Use a computer algebra system to verify your result.
(Multiple Choice)
4.9/5  (30)
(30)
The motion of a liquid in a cylindrical container of radius 1 is described by the velocity field . Find , where is the upper surface of the cylindrical container.
(Multiple Choice)
4.8/5  (45)
(45)
Showing 41 - 60 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)