Exam 10: Vector Functions
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
Let the position function of a particle be r (t) = sin 3t i+cos 3t j+sin 4t k. Find the smallest value of its speed.
(Multiple Choice)
4.8/5  (37)
(37)
Let the position function of a particle be . Find the smallest value of its speed.
(Multiple Choice)
4.8/5  (41)
(41)
Find the center of the osculating circle of the parabola at the origin.
(Short Answer)
4.9/5  (38)
(38)
Identify the geometric object that is represented by parametric equations .
(Multiple Choice)
4.9/5  (44)
(44)
Find the unit tangent vector T(t) to the curve r (t) = when t = 0.
(Multiple Choice)
4.8/5  (41)
(41)
Find the unit tangent vector T(t) to the curve r (t) = when t = 0.
(Multiple Choice)
4.9/5  (27)
(27)
Let the acceleration of a particle be , and let its velocity when t = 0 be . Find its speed when t = 2.
(Multiple Choice)
4.9/5  (37)
(37)
Consider r (t), the vector function describing the curve shown below. Put the curvatures at A, B, and C in order from smallest to largest. 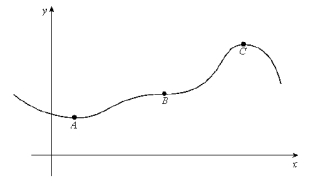
(Short Answer)
4.8/5  (41)
(41)
Find the equation of the osculating circle of the ellipse whose equation is given by
(Essay)
4.8/5  (45)
(45)
For , find and , the tangential and normal components of acceleration.
(Essay)
4.9/5  (40)
(40)
Showing 101 - 111 of 111
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)