Exam 10: Vector Functions
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
At what point does the curve have maximum curvature? What is the maximum curvature?
(Essay)
4.8/5  (32)
(32)
Find a parametric representation for the surface consisting of that part of the plane z = x + 3 that lies inside the cylinder .
(Essay)
4.8/5  (28)
(28)
Consider the curve in the xy-plane defined parametrically by x = t3 - 3t, y = t2, z = 0. Sketch a rough graph of the curve. 
(Essay)
4.8/5  (40)
(40)
Find the unit tangent vector T(t) to the curve r (t) = when t = 0.
(Multiple Choice)
4.7/5  (31)
(31)
Find the tangent vector (t) of the function r (t) = when t = .
(Multiple Choice)
4.8/5  (40)
(40)
Let the position function of a particle be . Find the velocity of the particle when t = 1.
(Multiple Choice)
4.8/5  (42)
(42)
Find a parametric representation for the surface consisting of that part of the elliptic paraboloid that lies in front of the plane x = 0.
(Essay)
4.8/5  (31)
(31)
Find the unit tangent vector T(t) to the curve r (t) = when t = 1.
(Multiple Choice)
4.7/5  (32)
(32)
Identify the surface with the vector equation . (Hint: First consider .)
(Short Answer)
4.7/5  (33)
(33)
A picture of a circular cylinder with radius a and height h is given below. Find a parametric representation of the cylinder. 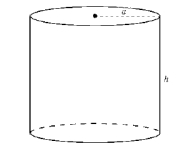
(Essay)
4.8/5  (29)
(29)
Identify the geometric object that is represented by parametric equations .
(Multiple Choice)
4.8/5  (28)
(28)
A particle is traveling along a helix whose vector equation is given by . Show that its velocity and acceleration are orthogonal at all times.
(Short Answer)
4.8/5  (40)
(40)
The graphs of which three of the following four vector functions lie along the line y = 4 - x?
(Multiple Choice)
4.7/5  (30)
(30)
Showing 21 - 40 of 111
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)