Exam 20: The Curl and Stokes Theorem

Let $\vec { G } ( x , y , z ) = - y \vec { i } + x \vec { j } + 3 x y z \vec { k }$ .Calculate div $\vec { G }$ .

The trumpet surface, S, is given parametrically by 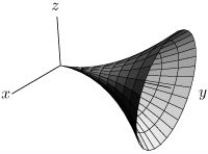$\vec { r } ( s , t ) = s \vec { 2 } \cos t \vec { i } + s \vec { j } + s ^ { 2 } \sin t k , 0 £ s £ 5,0 £ t £ 2 \pi$ If S has outward pointing normal, use an appropriate line integral to calculate $\hat { Q } { \operatorname { curl } } ( z \vec { i } + \cos ( x + z ) \vec { j } - x \vec { k } ) \times \vec { d A }$

Suppose $\int _ { S } \vec { F } \cdot d \vec { A } = \int _ { S } ( 4 x \vec { i } - 6 y \vec { j } + 2 z \vec { k } ) \cdot d \vec { A }$ for any closed surface S in space with outward-pointing normal.What does this tell you about $\text { div } \vec { F } \text { ? }$

For the following integral, say whether Stokes' Theorem, the Divergence Theorem, or neither applies. $\dot { \mathrm { Q } } ^ { \operatorname { curl } } \left( 2 x \vec { i } + z \vec { j } + 2 y ^ { 3 } \vec { k } \right) \times \vec{ d A }$ where S is a triangular plane in space oriented $\text { dow nw ard. }$

Using either Stokes' theorem or the Divergence theorem (whichever is appropriate), evaluate $\dot{\mathrm{Q}}((2 x+\cos y z) \vec{i}+(5 y+\sin 2 z) \vec{j}+(3 z+x) \vec{k}) \times d \vec{A}$ where S is the sphere of radius 2 oriented outward and centered at the point $\left( 2 , e ^ { - 25 } , \pi ^ { 2 } \right)$

Using either Stokes' theorem or the Divergence theorem (whichever is appropriate), evaluate the following: $\mathrm { Q } ( - 4 x \vec { i } + 3 y \vec { j } + 3 z \vec { k } ) \times \vec { d r }$ where C is a closed loop parameterized by $\vec { r } ( t ) = ( \cos t + \sin t ) \vec { i } + \cos ^ { 3 } t \vec { j } + \sin ^ { 4 } t \vec { k }$

Let $\vec {F }$ be a smooth velocity vector field describing the flow of a fluid.Suppose that $\operatorname { div } \vec { F } ( 1,2 , - 1 ) = 10$ Will there be an inflow or outflow of fluid at the point (1, 2,-1)?

Let $\vec { G }$ be a smooth vector field with $\operatorname { div } \vec { G } = 3$ at every point in space and let S₁ and S₂ be spheres of radius r, oriented outward, centered at (0,0,0)and at (1,2,1), respectively. $\int _ { s _ { 1 } } \vec { G } \cdot d \vec { A } = \int _ { S _ { 2 } } \vec { G } \cdot d \vec { A }$ .

An oceanographic vessel suspends a paraboloid-shaped net below the ocean at depth of $750$ feet, held open at the top by a circular metal ring of radius $30$ feet, with bottom $70$ feet below the ring and just touching the ocean floor.Set up coordinates with the origin at the point where the net touches the ocean floor and with z measured upward.

Let

If $\operatorname { div } \vec { F } = - 7$ everywhere and S is a smooth surface (oriented outward)enclosing a volume W of size V find $\int _ { S } \vec { F } \cdot \vec { d A }$ .

Let ${ \vec { F } } = - 3 x z \vec { i } + 4 ( y - x ) \vec { j } + 4 x \vec { k }$ (a)By direct computation, find the circulation of $\vec { F }$ around the circle of radius a, $\vec { r } ( t ) = \alpha \cos t \vec { i } + \alpha \sin t \vec { j }$ for 0 $\le$ t $\le$ 2 $\pi$ . (b)Use this result to find the $\vec { k }$ component of $\operatorname { curl } \vec { F } ( 0,0,0 )$

Let $\vec { F} = - 4 Z \vec { k }$ (a)Compute $\operatorname { div } \vec { F } ( 0,0,0 )$ . (b) By direct computation, find the flux of $\vec { F }$ through a cube with edge length l, centered at the origin and edges parallel to the axes. (c)Explain how your answers in parts (b)are related to that of part (a).

Suppose that $f ( x , y , z )$ is defined and differentiable everywhere and satisfies the differential equation $x \frac { \partial f } { \partial x } + y \frac { \partial f } { \partial y } + z \frac { \partial f } { \partial z } = 0$ .Let ${ \vec { F } } = f ( x , y , z ) \vec { r }$ , where $\vec { r } = x \vec { i } + y \vec { j } + z \vec { k }$ .Suppose that S is a closed surface and W is its interior.Find Q in the following equation: $\int _ { S } \vec { F } \cdot d \vec { A } = Q \int _ { W } f ( x , y , z ) d V$ .

Suppose that curl $\vec { F } ( 1,2,1 ) = 3 \vec { i } - 2 \vec { j } + - 5 \vec { k }$ curl $\vec { F } ( 0,2,1 ) = 6 \vec { i } + 2 \vec { j } + 5 \vec { k }$ and curl ${ \vec { F } } ( 1,3 , - 1 ) = - 3 \vec { i } + 2 \vec { j } + 10 \vec { k }$ Estimate the following line integrals. (a) $\int _ { C _ { 1 } } \vec { F } \cdot d \vec { r }$ where C₁ is given by $\vec { r } ( t ) = \vec { i } + ( 3 + 0.1 \cos t ) \vec { j } + ( 0.1 \sin t - 1 ) \vec { k } , \quad 0 \leq t \leq 2 \pi$ (b) $\int _ { c _ { 2 } } \vec { F } \cdot d \vec { r }$ where C₂ is given by $\vec { r } ( t ) = 0.1 \sin t \vec { i } + 2 \vec { j } + ( 1 + 0.1 \cos t ) \vec { k } , 0 \leq t \leq 2 \pi$ (c) $\int _ { C _ { 3 } } \vec { F } \cdot d \vec { r }$ where C₃ is given by $\vec { r } ( t ) = ( 1 + 0.1 \cos t ) \vec { i } + ( 2 + 0.1 \sin t ) \vec { j } + \vec { k } , \quad 0 \leq t \leq 2 \pi$

Use the Divergence Theorem to find the flux of the vector field $\vec { F } = \left( 4 x ^ { 3 } + 4 y z \right) \vec { i } + \left( 4 y ^ { 3 } + 8 x z \right) \vec { j } + \left( 4 z ^ { 3 } + 16 y x \right) \vec { k }$ through the cube 0 $\le$ x $\le$ 1, 0 $\le$ y $\le$ 1, 0 $\le$ z $\le$ 1.

Let $\left. \vec { F } = \left( e ^ { y } + 6 x \right) \right) \vec { i } + \left( 6 y + z \cos x ^ { 6 } \right) \vec { j } + ( 5 z + 6 x ) \vec { k }$ Calculate div $\vec { F} .$

Let $\vec { F }$ be a smooth velocity vector field describing the flow of a fluid.Suppose that $\operatorname { div } \vec { F } ( 1,2 , - 1 ) = - 4$ Estimate the value of $\int _ { S }{ \vec { F } } \cdot \vec{ d A }$ where S is a sphere of radius 0.25 centered at (1, 2,-1)oriented outward.Give your answer to 4 decimal places.

For the following integral, say whether Stokes' Theorem, the Divergence Theorem, or neither applies. $\hat { Q } \left( 2 x \vec { i } + z \vec { j } + 5 y ^ { 3 } \vec { k } \right) \times \vec{ d r }$ where S is a triangular plane in space oriented upward.

Let $\vec { a } = a _ { 1 } \vec { i } + \alpha _ { 2 } \vec { i } + \alpha _ { 3 } \vec { i }$ be a constant vector and f(x, y, z)be a smooth function.Which statement is true?