Exam 16: Integrating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
The region W is shown below.Write the limits of integration for in spherical coordinates. 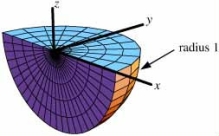
(Multiple Choice)
4.8/5  (40)
(40)
Set up an iterated integral for , where W is the solid region bounded below by the rectangle 0 x 3, 0 y 1 and above by the surface
(Multiple Choice)
4.9/5  (22)
(22)
Let W be the region between the spheres and .Given that , evaluate the integral , where is the region between the ellipsoids and .
(Multiple Choice)
4.9/5  (32)
(32)
Estimate R f(x, y)dA using the table of values below, where R is the rectangle 0 x 4, 0 y 6
y x 0 3 6 0 2 3 4 2 6 4 3 4 18 14 12
(Short Answer)
4.9/5  (39)
(39)
Consider the change of variables x = s + 3t, y = s - 2t.
Let R be the region bounded by the lines 2x + 3y = 1, 2x + 3y = 4, x - y = -3, and x - y = 2.Find the region T in the st-plane that corresponds to region R.
Use the change of variables to evaluate
(Short Answer)
4.8/5  (27)
(27)
Let x and y have joint density function Find the probability that 0.5 x 0.6.
(Short Answer)
4.8/5  (37)
(37)
Reverse the order of integration for the following integral.
(Multiple Choice)
4.9/5  (38)
(38)
Let R be the ice-cream cone lying inside the sphere and inside the cone .Find the center of mass of R.
(Essay)
4.9/5  (39)
(39)
Jane and Mary will meet outside the library at noon.Jane's arrival time is x and Mary's arrival time is y, where x and y are measured in minutes after noon.The probability density function for the variation in x and y is After Jane arrives, she will wait up to 15 minutes for Mary, but Mary won't wait for Jane.Find the probability that they meet.
(Short Answer)
4.8/5  (32)
(32)
An arrow strikes a circular target at random at a point (x, y), using a coordinate system with origin at the center of the target.The probability density function for the point where the arrow strikes is given by What is the probability that the arrow strikes within 0.45 feet of the center of the target.
(Short Answer)
4.8/5  (38)
(38)
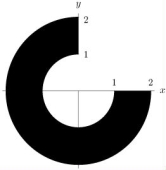
Calculate the following integral: where R is the shaded region shown below.
· 
(Essay)
4.8/5  (40)
(40)
Find the condition on the non-negative constants a and b for p(x, y)to be a joint density function, where
(Essay)
4.8/5  (37)
(37)
Choose the most appropriate coordinate system and set up a triple integral, including limits of integration, for a density function f(x, y, z)over the given region. 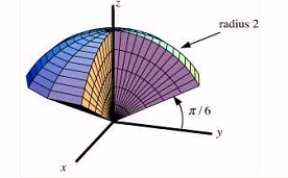
(Multiple Choice)
4.8/5  (31)
(31)
Find the volume of the solid bounded by the paraboloid and the plane z = 1.
(Essay)
4.8/5  (43)
(43)
Showing 21 - 40 of 76
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)