Exam 14: Differentiating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
A partial derivative is a specific example of a directional derivative.
(True/False)
4.8/5  (45)
(45)
Let .Find the instantaneous rate of change of f at the point in the direction of the point .
(Essay)
4.9/5  (32)
(32)
Given that , in which of the following directions does g increase the fastest?
(Multiple Choice)
4.8/5  (30)
(30)
If x(u, v)= uv and y(u, v)= u + 3v.
If H(u, v)= f(x(u, v), y(u, v)), what is Hv(0,-2)? Give your answer to 4 decimal places.
(Essay)
4.8/5  (32)
(32)
The quadratic Taylor approximations of at the points , (2,0)and (0,2)are given respectively by: (x,y)=-3+3(x+1+4(y+1 (x,y)=1-3(x-1+4(y-1 (x,y)=-2-9(x-2)-6(x-2-2 (x,y)=8+3x+24(y-2)+22(y-2 Determine fy
.
(Essay)
4.8/5  (40)
(40)
The tangent plane to the surface at any point passes through the origin.
(True/False)
4.9/5  (38)
(38)
The depth of a pond at the point with coordinates (x, y)is given by .(Assume that x, y, and h are measured in feet.)If a boat at the point (-3, -5)is sailing in the direction of the vector ,
then at what rate is the depth changing?
(Essay)
4.9/5  (37)
(37)
Arrange the following quantities in ascending order.(The level curves of are shown in the figure.Assume that the scales on the x- and y-axes are the same.) 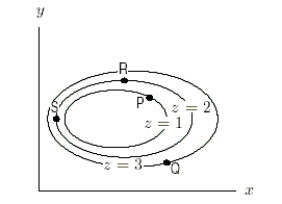
(Essay)
4.8/5  (42)
(42)
Find the equation of the tangent plane to the surface at (1, -3, 2).
(Multiple Choice)
4.8/5  (33)
(33)
The quantity z can be expressed as a function of x and y as follows: z = f(x, y).Now x and y are themselves functions of r and , as follows: and Suppose you know that g(1, /2)= -1, and h(1, /2)= 1.In addition, you are told that (-1,1)=1,(-1,1)=6, 1, =7 1, =7, 1, =6, 1, =4 Find
(Essay)
4.8/5  (36)
(36)
Suppose that the price P (in dollars)to purchase a used car is a function of C, its original cost (in dollars), and its age A (in years).So P = f(C,A). What is the sign of
(Multiple Choice)
4.8/5  (29)
(29)
Let be a function of three variables with .Suppose that .Simplify .
(Multiple Choice)
4.9/5  (33)
(33)
Consider the level curves shown for the function z = f(x, y). 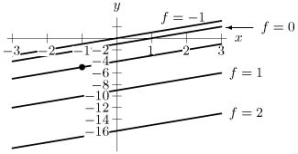 Determine the sign of
Determine the sign of
(Multiple Choice)
4.7/5  (31)
(31)
Find the directional derivative of at the point (3, 3, 2), in the direction of the vector
(Essay)
4.9/5  (37)
(37)
If x(u, v)= uv and y(u, v)= u + 4v.
If H(u, v)= f(x(u, v), y(u, v)), what is H(0,-1)? Give your answer to 4 decimal places.
(Short Answer)
4.9/5  (30)
(30)
Showing 21 - 40 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)