Exam 14: Differentiating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Let w = 3x cos y.If find w/ u and w/ v at the point .Give your answers to 2 decimal places.
(Essay)
4.9/5  (44)
(44)
Find the differential of the function at the point (3, 4).
A point is measured to be 3 units from the y-axis with an error of ±0.01 and 4 units from the x-axis with an error of ±0.02.Approximate the error in computing its distance from the origin.
(Essay)
4.9/5  (39)
(39)
Consider the surface given as the graph of .Let and let .Suppose that .Find the equation of the tangent plane to the surface at the point .
(Essay)
4.8/5  (35)
(35)
Consider the surface and the point .Find an equation for the plane tangent to the surface at P.
(Essay)
4.9/5  (38)
(38)
Find the following partial derivative: HP(2, 1)if Give your answer to 4 decimal places.
(Essay)
4.8/5  (40)
(40)
Suppose that as you move away from the point (2, 0, 2), the function increases most rapidly in the direction and the rate of increase of f in this direction is 7.At what rate is f increasing as you move away from (2, 0, 2)in the direction of ? Give your answer to 4 decimal places.
(Short Answer)
4.9/5  (38)
(38)
If is a unit vector and the level curves of f(x, y)are given below, then at point P we have 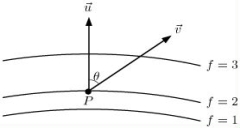
(True/False)
4.9/5  (39)
(39)
The quadratic Taylor approximations of at the points , (2,0)and (0,2)are given respectively by: (x,y)=-3+3(x+1+4(y+1 (x,y)=1-3(x-1+4(y-1 (x,y)=-2-9(x-2)-6(x-2-2 (x,y)=8+3x+24(y-2)+22(y-2 Find an approximate value of .
(Essay)
4.8/5  (28)
(28)
Let .What is the equation of the tangent plane to the graph of at the point ?
(Essay)
4.9/5  (30)
(30)
Suppose f(x, y)is a function of x and y and define Find given that and
(Essay)
4.8/5  (43)
(43)
The table below gives values of a function f(x, y)near x = 1, y = 2. 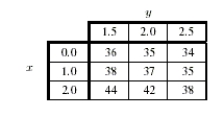 Estimate .
Estimate .
(Essay)
4.8/5  (37)
(37)
Suppose that Find an equation for the tangent plane to f at the point (3, 0).
(Multiple Choice)
4.9/5  (34)
(34)
Find the equation of the tangent plane to at the point (-4, 1, 3).
(Multiple Choice)
4.7/5  (40)
(40)
Find the points on the ellipsoid where the tangent plane is parallel to the plane .
(Essay)
4.9/5  (38)
(38)
Showing 41 - 60 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)