Exam 14: Differentiating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Suppose that is the temperature (in degrees Celsius)at the point (where x and y are in meters).If you are standing at the point and proceed in the direction of the point , will the temperature be increasing or decreasing at the moment you begin? At what rate? Give your answer to 4 decimal places.
(Essay)
4.7/5  (34)
(34)
Sally is on a day hike at Mt.Baker.From 9 to 11:00 a.m.she zig-zags up z = f(x, y)where x is the number of miles due east of her starting position, y is the number of miles due north of her starting position, and z is her elevation in miles above sea level.Feeling tired, she decides to continue walking, but in such a way that her altitude remains constant from 11 a.m.to noon to settle her stomach for lunch.At 11:30 a.m., she will be passing through (2, -1, 5)where fx(2, -1)= 3 and fy(2, -1)= -2.
What is the slope of her "path" in the x, y plane at this instant? (This "path" is among the level curves in the plane.)
(Essay)
4.7/5  (28)
(28)
The ideal gas law states that for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
A mole of a certain gas is at a temperature of 290° K, a pressure of 1 atmosphere, and a volume of 0.04 m3.
What is for this gas?
(Essay)
4.8/5  (32)
(32)
Let f be a differentiable function with local linearization L(x, y)= -1 + 4(x - 4)- 2(y - 2)at (4, 2).Evaluate f(4, 2).
(Short Answer)
4.9/5  (35)
(35)
In a neighborhood clinic, the number of patient visits can be described as a function of the number of doctors, x, and the number of nurses, y, by .With upcoming budget cuts, the clinic must reduce the number of doctors at the rate of 2 per month.Estimate the rate at which the number of nurses has to be increased in order to maintain the current patient load.Currently there are 30 doctors and 50 nurses.
(Essay)
4.9/5  (40)
(40)
Suppose that , with (a)What is the directional derivative of f at (1, -1)in the direction of ?
(b)What is the smallest value of the directional derivative of f at (1, -1)among all possible directions?
(Short Answer)
4.9/5  (37)
(37)
Below is a contour diagram for f(x, y)which is defined and continuous everywhere.The z-values have been omitted.Explain why it is true that . 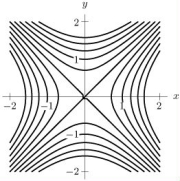
(Essay)
4.9/5  (31)
(31)
Let represent the surface area of a rectangular solid of length x, width y, and height z.Find and explain its meaning in terms of how the solid changes with respect to z.
(Essay)
4.7/5  (31)
(31)
Let represent the volume of a rectangular solid of length x, width y, and height z.Find and explain its meaning in terms of how the solid changes with respect to x.
(Essay)
4.7/5  (37)
(37)
The level curves of a function z = f(x, y)are shown below.Assume that the scales along the x and y axes are the same. 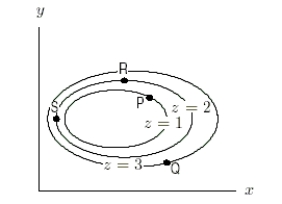
(True/False)
4.9/5  (39)
(39)
For the function find a unit vector in the direction of the steepest increase at the point (a, b)= (1, 1).
(Multiple Choice)
4.8/5  (37)
(37)
Suppose || f(a, b, c)||=19.Is it possible to choose a direction from (a, b, c)so that in that direction is -19?
(True/False)
4.9/5  (27)
(27)
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off.It is given that: f(100000,7,20)=775.29, f(100000,8,20)=836.44, f(100000,7,25)=706.77 f(120000,7,20)=930.35, f(120000,8,20)=1003.72, f(120000,7,25)=848.13 Estimate the value of and interpret your answer in terms of a mortgage payment.Select all answers that apply.
(Multiple Choice)
4.8/5  (43)
(43)
Let Find dz/dt at t = 1 using the chain rule.Give your answer to 4 decimal places.
(Essay)
4.8/5  (38)
(38)
The equations of the tangent planes to the graph z = f(x, y)at the points (0, -2), (2, 1)are and , respectively.Determine the value of State whether the value you find is exact or an approximation.
(Essay)
4.9/5  (36)
(36)
Suppose the graph of contains the point , and that the tangent plane at P is given by .Find and .
(Essay)
4.8/5  (40)
(40)
Suppose that there exists a linear function near the point (0,0)such that the difference between and approaches 0 as approaches (0,0).Then f is differentiable at (0,0)with as its local linearization.
(True/False)
4.8/5  (31)
(31)
The volume of a right circular cylinder is to be calculated from measured values of r and h.Suppose r is measured with an error of no more than 2.5% and h with an error of no more than 1%.Using differentials, estimate the percentage error in the calculation of V.
(In general, in measuring a quantity Q, the percentage error is dQ/Q.)
(Short Answer)
4.8/5  (27)
(27)
Showing 61 - 80 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)