Exam 14: Differentiating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Given the contour diagram shown below
(a)Sketch a graph of f(1, y).
(b)Sketch a graph of f(x, 0). 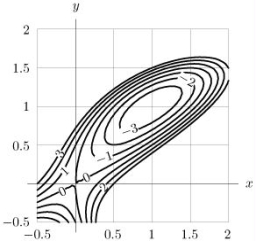
(Essay)
4.8/5  (29)
(29)
In an electric circuit, two resistors (of resistance R1 and R2, respectively)are connected so that the combined resistance of the circuit, R, is given by Find .
(Essay)
4.7/5  (38)
(38)
Given that and Suppose that f(1, 1)= 4.Find the quadratic Taylor polynomial of f(x, y)at (1, 1).
(Essay)
4.8/5  (35)
(35)
Suppose that fx(2, 1)= 2.2, fx(2.5, 1)= 1, fx(2, 1.5)= 1.8, fy(2, 1)= -0.8, fy(2.5, 1)= -1.2 and fy(2, 1.5)= -1.4.
If estimate the value of f(1.85, 0.8)using a quadratic Taylor polynomial about (2,1).
Use difference quotients to approximate all second derivatives.
(Short Answer)
4.8/5  (25)
(25)
For the function g(x, y)with contour diagram below: 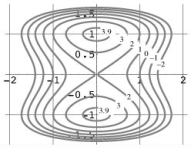 Find the direction in which g is increasing the fastest at the point (1, 1).
Find the direction in which g is increasing the fastest at the point (1, 1).
(Essay)
4.8/5  (32)
(32)
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off.It is given that: f(100000,7,20)=775.29, f(100000,8,20)=836.44, f(100000,7,25)=706.77 f(120000,7,20)=930.35, f(120000,8,20)=1003.72, f(120000,7,25)=848.13 Estimate the value of
(Essay)
4.8/5  (37)
(37)
Suppose .
Use a difference quotient to estimate and with h = 0.01.Give your answers to 3 decimal places.
(Essay)
4.9/5  (34)
(34)
Showing 121 - 129 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)