Exam 4: Using the Derivative
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
If you throw a stone into the air at an angle of to the horizontal, it moves along the curve , where y is the height of the stone above the ground, x is the horizontal distance.If the angle is fixed, what value of x gives the maximum height? (Your answer will .)
(Multiple Choice)
4.8/5  (31)
(31)
A water tank is constructed in the shape of a sphere seated atop a circular cylinder.If water is being pumped into the tank at a constant rate, let be the height of the water as a function of time.Which of the following is true at the point where b? 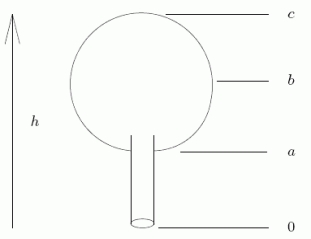
(Multiple Choice)
4.9/5  (30)
(30)
Frank decided to ride in a hot air balloon.His brother Damien was going to videotape the lift off from a distance of 30 feet away.The hot air balloon rises to a height of 2000 feet in 19 minutes.What is the rate at which the camera's angle should be raised in order to follow the balloon? (specify units)
(Essay)
4.7/5  (33)
(33)
Find the quantity q which maximizes profit if the total revenue, R(q), and the total cost, C(q), are given in dollars by , where units.
Round to the nearest whole number.
(Short Answer)
4.9/5  (34)
(34)
Find the marginal cost for q = 100 when the fixed costs in dollars are 1000, the variable costs are $190 per item, and each sells for $310.
(Short Answer)
4.8/5  (31)
(31)
A lady bug moves on the xy-plane according the the equations , . When is the lady bug ever moving straight up or down?
(Multiple Choice)
4.8/5  (30)
(30)
Consider a continuous function with the following properties: 
 for
for  . Which of the following is true?
. Which of the following is true?
(Multiple Choice)
4.9/5  (46)
(46)
A fan is watching a 100-meter footrace from a seat in the bleachers 15 meters back from the midway point.The winning runner is moving approximately 8 meters per second.How fast is the distance from the fan to the winning runner changing when he is x meters into the race?
(Essay)
4.7/5  (29)
(29)
Below is the graph of the derivative of a function f, i.e., it is a graph of y = f '(x).Where in the interval 0 x 4 does f achieve its global maximum? 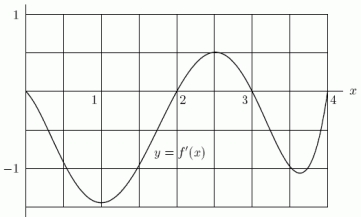
(Multiple Choice)
4.9/5  (30)
(30)
Below is the graph of the rate r at which people arrive for lunch at Cafeteria Charlotte.Checkers start at 12:00 noon and can pass people through at a constant rate of 5 people/minute.Let f(t)be the length of the line (i.e.the number of people)at time t.Suppose that at 11:50 there are already 150 people lined up.Using the graph together with this information, when is the line the longest? 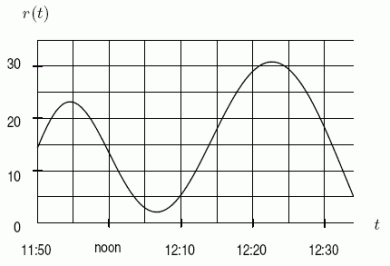
(Short Answer)
4.7/5  (32)
(32)
The revenue for selling q items is and the total cost is C(q)= 110 + 60q.Which function gives the total profit earned?
(Multiple Choice)
4.9/5  (42)
(42)
Which of the following parametric equations pass through the points (8, 1)and (-1, -1)?
(Multiple Choice)
4.8/5  (35)
(35)
The cost C(q)(in dollars)of producing a quantity q of a certain product is shown in the graph below.Suppose that the manufacturer can sell the product for $2.50 each (regardless of how many are sold), so that the total revenue from selling a quantity q is R(q)= 2.5q.The difference is the total profit.Let be the quantity that will produce the maximum profit.What is ? 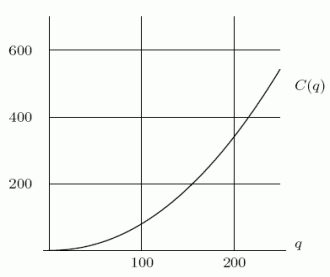
(Short Answer)
4.7/5  (37)
(37)
The equations describe the motion of a particle moving on a circle.Assume x and y are in miles and t is in days.What is the speed of the particle (in miles per day)when it passes through the point (-9/ , 0)? Round to 3 decimal places.
(Short Answer)
4.8/5  (35)
(35)
Total cost and revenue are approximated by the functions C = 1200 + 3.5q and R = 6q, both in dollars.Identify the marginal cost per item.
(Short Answer)
4.9/5  (32)
(32)
A spherical lollipop has a circumference of 7.9 centimeters.A student decides to measure the rate of change of the volume of the lollipop, in per minute.The student licks the lollipop and measures the circumference every minute.The radius is decreasing at a rate of 0.18 cm/min.Determine the rate at which the volume is changing when the circumference is half of it's original size.[ ]
(Short Answer)
4.9/5  (39)
(39)
A lady bug moves on the xy-plane according the the equations , .
Suppose that the temperature at a point (x, y)in the plane depends only on the y coordinate of the point and is equal to .Find the rate of change of the temperature at the location of the lady bug at time t.
(Essay)
4.9/5  (36)
(36)
A student is drinking a milkshake with a straw from a cylindrical cup with a radius of 5.5 cm.If the student is drinking at a rate of 4.5 cm3 per second, then the level of the milkshake dropping at a rate of _____ cm per second.Round to 2 decimal places.
(Short Answer)
4.9/5  (40)
(40)
Showing 81 - 100 of 108
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)