Exam 12: Linear Regression and Correlation

In simple linear regression analysis, if the independent variable x and the dependent variable y are highly correlated, this does not only mean that they are linearly related, but it also means that a change in x will cause a change in y.

In a simple linear regression problem, if the coefficient of determination is 0.95, this means that 95% of the variation in the independent variable x can be explained by regression line.

A regression analysis between sales (in $1000) and advertising (in $) resulted in the following least squares line: 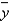= 80,000 + 5x. This implies that:

In a simple linear regression setting, the probabilistic model equation allows for some deviation of the points about the regression line, making it a more practical model.

If the coefficient of determination is 0.982, then the slope of the regression line must be positive.

The general manager of a chain of furniture stores believes that experience is the most important factor in determining the level of success of a salesperson. To examine this belief she records last month's sales (in $1,000s) and the years of experience of 10 randomly selected salespeople. These data are listed below. 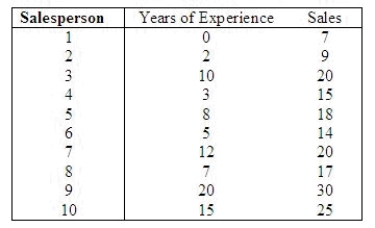Predict with 95% confidence the monthly sales of a salesperson with 10 years of experience. CI = ______________ Enter (n1, n2) in thousands Estimate with 95% confidence the average monthly sales of all salespersons with 10 years of experience. CI = ______________ Enter (n1, n2) in thousands Which interval in the previous two questions is narrower: the confidence interval estimate of the expected value of y or the prediction interval for the same given value of x (10 years) and same confidence level? ______________ Why? ________________________________________________________

A scientist is studying the relationship between x = density (in number per square meter) of aspen trees around a pond and y = beaver abundance. The following statistical software output is from a regression analysis for predicting y from x. 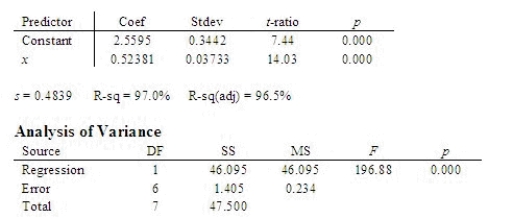What is the least-squares regression equation? 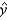= ______________ What is the estimated slope? b = ______________ What is the estimated y-intercept? a = ______________ What is the value of the error sum of squares? ______________ What is the value of the coefficient of determination? ______________ What is the percentage of variation in beaver abundance accounted for by regression on the density of aspen trees? ______________

Given a specific value of x and confidence level, which of the following statements is correct?

The least squares method for determining the best fit minimizes:

In a simple linear regression analysis, if SSE = 27, Total SS = 63, then the percentage of the variation in the dependent variable y that is explained by the independent variable x is about:

A company manager is interested in the relationship between x = number of years that an employee has been with the company and y = the employee's annual salary (in thousands of dollars). The following MINITAB output is from a regression analysis for predicting y from x for n = 15 data points. 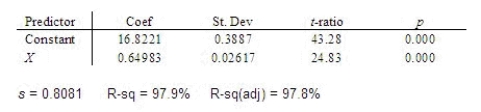What is the least squares regression equation? 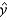= ______________ What are the least squares estimates of the slope? ______________ What are the least squares estimates of the y-intercept? ______________ Interpret the estimated slope. ________________________________________________________ Interpret the estimated y-intercept. ______________ What is the value of 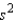? ______________ What is the value of the sum of squares for error (SSE)? ______________ Find the coefficient of determination. ______________ Interpret the coefficient of determination. ________________________________________________________ Does a linear relationship exist between x and y? Test using 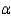= 0.05. What is the p-value? ______________ Conclude: ______________ A linear relationship ______________ exist between x and y.

If the coefficient of determination is 0.975, then the slope of the regression line:

Which of the following statements is true?

Let x be the number of pieces of furniture in a delivery truck and y be the time (in hours) it takes the delivery person to deliver all the pieces of furniture. A simple linear regression analysis related x and y where the least squares estimates of the regression parameters are a = 1.85 and b = 0.55. What is the least squares best-fitting regression line? 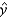= ______________ What is the slope of the equation? ______________ Interpret the slope of the equation. Does a positive slope make practical sense? Justify your answer. ________________________________________________________ What is the y-intercept? ______________ Interpret the y-intercept, does this make sense? ________________________________________________________ Use the least squares regression line to estimate the time it should take to deliver 10 pieces of furniture. (You may assume that 10 is in the range of the data.) ______________ (hours)

When regression analysis is used for prediction, the confidence interval for the average y given x will be wider than the prediction interval for a particular value of y given x.

If an estimated regression line has a y-intercept of 10 and a slope of 4, then when x = 2 the actual value of y is:

In order to predict with 98% confidence the expected value of y for a given value of x in a simple linear regression problem, a random sample of 15 observations is taken. Which of the following t-table values listed below would be used?

Six points have these coordinates: The normal probability plot and the residuals versus fitted values plots generated by Minitab are shown below. 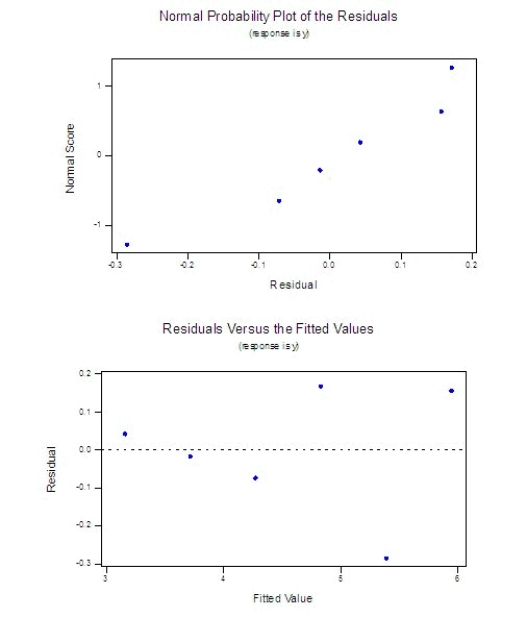Does it appear that any regression assumptions have been violated? ______________ Explain. ________________________________________________________

A regression line using 25 observations produced SSR = 118.68 and SSE = 56.32. The standard error of estimate was:

In simple linear regression, the plot of residuals versus fitted values 3 can be used to check for: