Exam 12: Linear Regression and Correlation
Exam 1: Describing Data With Graphs94 Questions
Exam 2: Describing Data With Numerical Measures186 Questions
Exam 3: Describing Bivariate Data35 Questions
Exam 4: Probability and Probability Distributions136 Questions
Exam 5: Several Useful Discrete Distributions129 Questions
Exam 6: The Normal Probability Distribution196 Questions
Exam 7: Sampling Distributions162 Questions
Exam 8: Large-Sample Estimation173 Questions
Exam 9: Large-Sample Tests of Hypotheses210 Questions
Exam 10: Inference From Small Samples261 Questions
Exam 11: The Analysis of Variance156 Questions
Exam 12: Linear Regression and Correlation165 Questions
Exam 13: Multiple Regression Analysis178 Questions
Exam 14: Analysis of Categorical Data136 Questions
Exam 15: Nonparametric Statistics198 Questions
Select questions type
The residuals are observations of the error variable 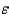 . Consequently, the minimized sum of squared deviations is called the sum of squares for error, denoted SSE.
. Consequently, the minimized sum of squared deviations is called the sum of squares for error, denoted SSE.
(True/False)
4.9/5  (40)
(40)
One way to measure the strength of the relationship between the response variable y and the predictor variable x is to calculate the coefficient of determination; that is, the proportion of the total variation in y that is explained by the linear regression of y on x.
(True/False)
4.8/5  (30)
(30)
In simple linear regression, if the estimated values 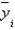 and the corresponding actual values
and the corresponding actual values 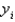 are equal, then the standard error of estimate, SE(
are equal, then the standard error of estimate, SE( 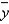 ), must equal -1.0.
), must equal -1.0.
(True/False)
4.7/5  (34)
(34)
The prediction interval developed from a simple linear regression model will be very narrow when the value of x used to predict y is equal to the mean value 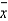 .
.
(True/False)
4.8/5  (39)
(39)
If the coefficient of determination value for a simple linear regression model is .90, then the correlation coefficient between the two variables will be .81.
(True/False)
4.9/5  (37)
(37)
In regression analysis, the independent variable is a variable whose value is known and is being used to explain or predict the value of another variable.
(True/False)
4.9/5  (38)
(38)
Which of the following statements is false regarding the residuals in simple linear regression model?
(Multiple Choice)
4.8/5  (37)
(37)
In simple linear regression, one can use the plot of residuals versus the fitted values of y to check for a constant variance as well as to make sure that the linear model is in fact adequate.
(True/False)
4.9/5  (30)
(30)
An indication of no linear relationship between two variables x and y would be:
(Multiple Choice)
4.9/5  (37)
(37)
The sign of the correlation coefficient in a simple linear regression model will always be the same as the sign of the y-intercept coefficient 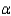 .
.
(True/False)
4.8/5  (36)
(36)
In simple linear regression, the plot of residuals versus fitted values 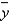 should:
should:
(Multiple Choice)
4.7/5  (38)
(38)
Evidence supports using a simple linear regression model to estimate a person's weight based on a person's height. Let x be a person's height (measured in inches) and y be the person's weight (measured in pounds). A random sample of eleven people was selected and the following data recorded:  The following output was generated for the data:
The following output was generated for the data: 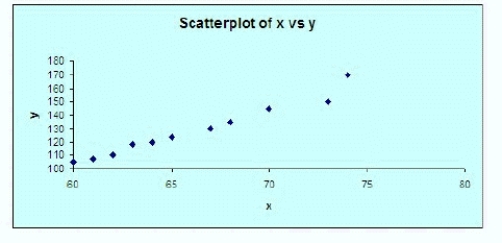 Based on the scatterplot above, does a simple linear regression model seem appropriate?
______________
Justify your answer.
________________________________________________________
Use the printout to find the least-squares prediction line.
Based on the scatterplot above, does a simple linear regression model seem appropriate?
______________
Justify your answer.
________________________________________________________
Use the printout to find the least-squares prediction line. 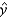 = ______________
Based on the printout, do there appear to be any outliers in the data?
______________
Justify your answer.
________________________________________________________
Consider the following residual plot of the residuals versus the fitted values.
= ______________
Based on the printout, do there appear to be any outliers in the data?
______________
Justify your answer.
________________________________________________________
Consider the following residual plot of the residuals versus the fitted values. 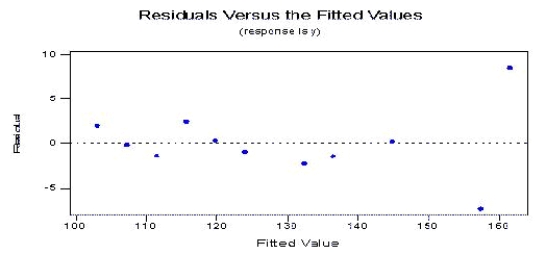 What conclusion, if any, can be drawn from the plot?
________________________________________________________
Consider the following normal probability plot of the residuals.
What conclusion, if any, can be drawn from the plot?
________________________________________________________
Consider the following normal probability plot of the residuals. 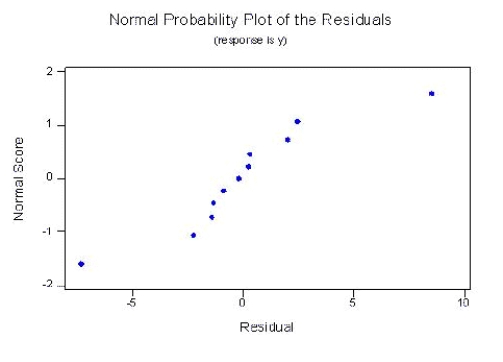 What conclusion can be drawn from the plot?
________________________________________________________
Based on the previous two plots, should you use the model in the computer printout to predict weight?
______________
Justify your answer.
________________________________________________________
What conclusion can be drawn from the plot?
________________________________________________________
Based on the previous two plots, should you use the model in the computer printout to predict weight?
______________
Justify your answer.
________________________________________________________
(Essay)
4.9/5  (39)
(39)
A professor of economics wants to study the relationship between income (y in $1000s) and education (x in years). A random sample eight individuals is taken and the results are shown below.  Determine the standard error of estimate.
sr = ______________
Describe what this statistic tells you about the regression line.
____________________________
Determine the coefficient of determination.
R2 = ______________
Discuss what its value tells you about the two variables.
________________________________________________________
Calculate the Pearson correlation coefficient.
r = ______________
Why does it have the sign it has?
________________________________________________________
Conduct a test of the population slope to determine at the 5% significance level whether a linear relationship exists between years of education and income.
Test statistic:
t = ______________
Rejection Region:
Reject H0 if | t | > ______________
Conclusion:
______________
A linear relationship ______________ between years of education and income.
Determine the standard error of estimate.
sr = ______________
Describe what this statistic tells you about the regression line.
____________________________
Determine the coefficient of determination.
R2 = ______________
Discuss what its value tells you about the two variables.
________________________________________________________
Calculate the Pearson correlation coefficient.
r = ______________
Why does it have the sign it has?
________________________________________________________
Conduct a test of the population slope to determine at the 5% significance level whether a linear relationship exists between years of education and income.
Test statistic:
t = ______________
Rejection Region:
Reject H0 if | t | > ______________
Conclusion:
______________
A linear relationship ______________ between years of education and income.
(Essay)
4.7/5  (42)
(42)
In a simple linear regression problem, if the coefficient of determination is 0.96, this means that:
(Multiple Choice)
4.7/5  (32)
(32)
In publishing the results of some research work, the following values of the correlation coefficient were listed. Which one would appear to be incorrect?
(Multiple Choice)
4.9/5  (31)
(31)
In a simple linear regression problem including n = 10 observations, which of the following table values would be appropriate for a 95% confidence interval estimation for the average value of y?
(Multiple Choice)
4.8/5  (37)
(37)
In a simple linear regression problem, the following statistics are calculated from a sample of 10 observations: 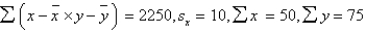 . The least squares estimates of the slope and y-intercept are respectively:
. The least squares estimates of the slope and y-intercept are respectively:
(Multiple Choice)
4.8/5  (32)
(32)
When the actual values y of a dependent variable and the corresponding predicted values 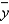 are the same, the standard error of estimate
are the same, the standard error of estimate 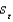 will be -1.0.
will be -1.0.
(True/False)
4.8/5  (37)
(37)
Showing 101 - 120 of 165
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)