Exam 3: The Derivative and the Tangent Line Problem

Find the second derivative of the function. $f ( x ) = \left( 3 x ^ { 3 } + 7 \right) ^ { 7 }$

A conical tank (with vertex down) is feet across the top and feet deep. If water is flowing into the tank at a rate of cubic feet per minute, find the rate of change of the Depth of the water when the water is feet deep.

$\text { Find the derivative of the function } y = \ln \sqrt { x ^ { 2 } - 7 } \text {. }$

$\text { Find an equation of the tangent line to the graph of } y = \ln \left( x ^ { 3 } \right) \text { at the point } ( 1,0 ) \text {. }$

Suppose the position function for a free-falling object on a certain planet is given by $s ( t ) = - 12 t ^ { 2 } + v _ { 0 } t + s _ { 0 }$ . A silver coin is dropped from the top of a building that is 1372 feet tall. Find the instantaneous velocity of the coin when $t = 4$ .

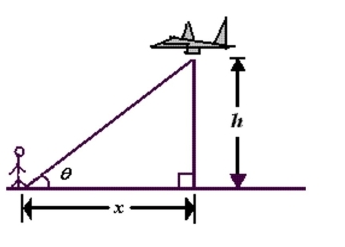
airplane flies at an altitude of 14 miles toward a point directly over an observer. Consider $\theta$ and $x$ as shown in the following figure. Write $\theta$ as a function of $x$ .

The displacement from equilibrium of an object in harmonic motion on the end of a spring is $y = \frac { 1 } { 4 } \cos 8 t - \frac { 1 } { 3 } \sin 15 t$ where $y$ is measured in feet and $t$ is the time in seconds. Determine the position of the object when $t = \pi / 12$ . Round your answer to two decimal places.

$\text { The volume of a cube with sides of length } s \text { is given by } V = s ^ { 3 } \text {. Find the rate of }$ change of volume with respect to $s$ when $s = 6$ centimeters.

Approximate the positive zero(s) of the function $f ( x ) = x ^ { 3 } - \cos x \text { to three decimal }$ places. Use Newton's Method and continue the process until two successive approximations differ by less than 0.001. $0.001$

$\text { Find } \frac { d y } { d x } \text { by implicit differentiation given that } 2 x y = 9 \text {. }$

$\text { Find the derivative of the function } f ( x ) = \frac { 6 } { \sqrt [ 2 ] { x } } \text { by the limit process. }$

$\text { Use the Quotient Rule to differentiate the function } f ^ {t } ( x ) = \frac { 4 + x } { x ^ { 2 } + 9 } \text {. }$

$\text { Differentiate } 7 x ^ { 2 } - 7 x y ^ { 2 } + 8 y ^ { 3 } = 16 \text { with respect to } t ( x \text { and } y \text { are functions of } t \text { ). }$

Suppose the position function for a free-falling object on a certain planet is given by $s ( t ) = - 13 t ^ { 3 } + v _ { 0 } t + s _ { 0 }$ . A silver coin is dropped from the top of a building that is 1370 feet tall. Determine the velocity function for the coin.

Suppose the position function for a free-falling object on a certain planet is given by $s ( t ) = - 12 t ^ { 2 } + v _ { 0 } t + s _ { 0 }$ . A silver coin is dropped from the top of a building that is 1372 feet tall. Find the time required for the coin to reach ground level. Round your answer to the three decimal places.

Find the derivative of the function. $f ( x ) = x ^ { 4 }$

$\text { Approximate the fixed point of the function } f ( x ) = \cos x \text { between } - \frac { \pi } { 2 } \text { and } \frac { \pi } { 2 } \text { to two }$ decimal places. (A fixed po int $x _ { 0 }$ of a function $f$ is a value of $x$ such that $f \left( x _ { 0 } \right) = x _ { 0 }$ .)

A ball is thrown straight down from the top of a 300-ft building with an initial velocity of $- 12 \mathrm { ft }$ per second. The position function is $s ( t ) = - 16 t ^ { 2 } + v _ { 0 } t + s _ { 0 }$ . What is the velocity of the ball after 4 seconds?

$\text { Describe the } x \text {-values at which the graph of the function } f ( x ) = \frac { x ^ { 2 } } { x ^ { 2 } - 9 } \text { given below }$ is differentiable.

$\text { Find } \frac { d ^ { 2 } y } { d x ^ { 2 } } \text { in terms of } x \text { and } y \text {. }$ $x ^ { 2 } + y ^ { 2 } = 6$