Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
A projectile is shot upwards from the surface of the earth with an initial velocity of 108 meters per second. The position function is What is its velocity after 7 seconds?
(Multiple Choice)
4.9/5  (34)
(34)
Find the rate of change of the distance between the origin and a moving point on the graph of if centimeters per second.
(Multiple Choice)
4.9/5  (38)
(38)
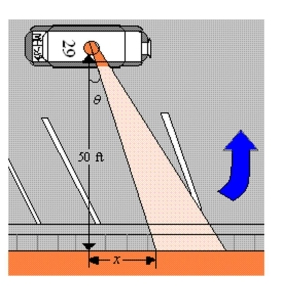
A petrol car is parked 50 feet from a long warehouse (see figure). The revolving light on top of the car turns at a rate of 30 revolutions per minute. How fast is the light beam moving along the wall when the beam makes an angle of with the perpendicular from the light to the wall.
(Multiple Choice)
5.0/5  (33)
(33)
it. The buoy moves a total of feet (vertically) between its low point and its high point. It returns to its high point every 14 seconds. Write an equation describing the motion of the buoy if it is at its high point at .
(Multiple Choice)
4.8/5  (42)
(42)
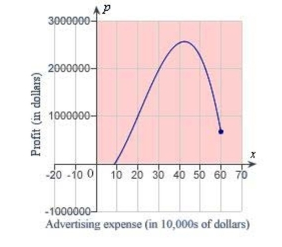
A manufacturer of digital audio players estimates that the profit for selling a particular model is , where is the profit in dollars and is the advertising expense in 10,000 's of dollars (see figure). Find the smaller of two advertising amounts that yield a profit of . Round your answer to the nearest dollar. Advertising expense (in 10,000 s of dollars)
(Multiple Choice)
4.8/5  (38)
(38)
Use Newton's Method to approximate the zero(s) of the function accurate to three decimal places.
(Multiple Choice)
4.7/5  (30)
(30)
cost of goods or services during any year in that decade is where is the time in years and is the present cost. The price of an oil change for your car is presently . Find the rate of change of with respect to when . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (33)
(33)
time in seconds and the dimensions are in inches. Find the rate of change of the volume of the cylinder, V, with respect to time.
(Multiple Choice)
4.9/5  (31)
(31)
Find the slope of the graph of the function at the given value. when
(Multiple Choice)
4.9/5  (36)
(36)
Use the alternative form of the derivative to find the derivative of the function
(Multiple Choice)
4.8/5  (25)
(25)
Given the derivative below find the requested higher-order derivative.
(Multiple Choice)
4.7/5  (39)
(39)
Showing 41 - 60 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)