Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
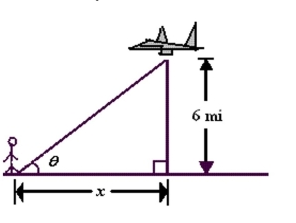
airplane flies at an altitude of 6 miles towards a point directly over an observer. Consider and as shown in the following figure. The speed of the plane is 400 miles per hour.
Find when . Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (38)
(38)
Suppose that the total number of arrests T (in thousands) for all males ages 14 to 27 in 2006 is approximated by the model where is the age in years (see figure). Approximate the two ages to one decimal place that had total arrests of 275 thousand. 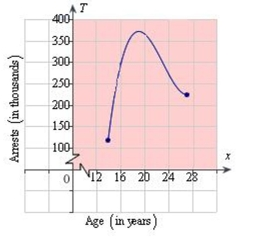
(Multiple Choice)
4.9/5  (42)
(42)
Find the slope of the graph of the function at the given value. when
(Multiple Choice)
4.9/5  (33)
(33)
The displacement from equilibrium of an object in harmonic motion on the end of a spring is where is measured in feet and is the time in seconds. Determine the velocity of the object when . Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (36)
(36)
A population of 620 bacteria is introduced into a culture and grows in number according to the equation where is measured in hours. Find the rate at which the population is growing when . Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (35)
(35)
Newton's Method to approximate the zero(s) of the function accurate to three decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Showing 81 - 100 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)