Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Use the alternative form of the derivative to find the derivative of the function
(Multiple Choice)
4.9/5  (24)
(24)
Suppose a 15-centimeter pendulum moves according to the equation where is the angular displacement from the vertical in radians and is the time in seconds. Determine the rate of change of when seconds. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Find the slope of the graph of the function at the given value. at
(Multiple Choice)
4.8/5  (43)
(43)
cost of goods or services during any year in that decade is where is the time in years and is the present cost. The price of an oil change for your car is presently . Estimate the price 3 years from now. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (35)
(35)
Suppose the position function for a free-falling object on a certain planet is given by . A silver coin is dropped from the top of a building that is 1372 feet tall. Determine the average velocity of the coin over the time interval .
(Multiple Choice)
4.8/5  (38)
(38)
Find the derivative of the following function using the limiting process.
(Multiple Choice)
4.9/5  (47)
(47)
Find the derivative of the following function using the limiting process.
(Multiple Choice)
4.7/5  (36)
(36)
A ladder feet long is leaning against the wall of a house (see figure). The base of the ladder is pulled away from the wall at a rate of feet per second. How fast is the top of the ladder
Moving down the wall when its base is feet from the wall? Round your answer to two decimal
Places. 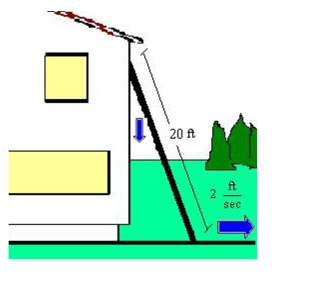
(Multiple Choice)
4.8/5  (41)
(41)
Showing 161 - 180 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)