Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the points at which the graph of the equation has a vertical or horizontal tangent line.
(Multiple Choice)
4.8/5  (39)
(39)
The radius r of a sphere is increasing at a rate of inches per minute. Find the rate of change of the volume when
(Multiple Choice)
4.9/5  (35)
(35)
Use implicit differentiation to find an equation of the tangent line to the ellipse
(Multiple Choice)
5.0/5  (38)
(38)
In a free-fall experiment, an object is dropped from a height of 144 feet. A camera on the ground 500 feet from the point of impact records the fall of the object as shown in the figure. Assuming the object is released at time . Find the rate of change of the angle of elevation of the camera when . Round your answer to four decimal places.
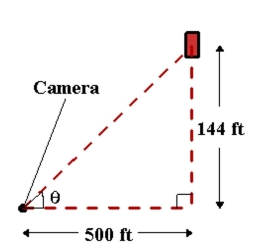
(Multiple Choice)
4.8/5  (42)
(42)
Apply Newton's Method to approximate the x-value of the indicated point of intersection of differ by less than 0.001. (Hint: Let .) Round your answer to three decimal places.
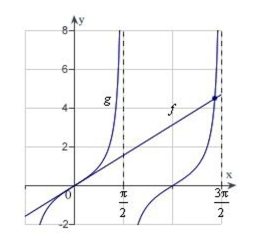
(Multiple Choice)
4.7/5  (33)
(33)
When satellites observe Earth, they can scan only part of Earth's surface. Some satellites have sensors that can measure the angle shown in the figure. Let represent the satellite's distance from Earth's surface and let represent Earth's radius. Find the rate at which is changing with respect to when (Assume miles.) Round your answer to the nearest unit.
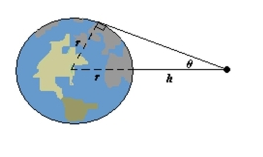
(Multiple Choice)
4.8/5  (35)
(35)
the dimensions are in inches. Find the rate of change of area, A, with respect to time.
(Multiple Choice)
4.9/5  (36)
(36)
Showing 61 - 80 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)