Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
A petrol car is parked 40 feet from a long warehouse (see figure). The revolving light on top
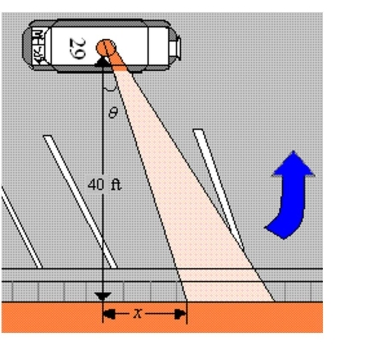
(Multiple Choice)
5.0/5  (27)
(27)
Find an equation to the tangent line for the graph of f at the given point.
(Multiple Choice)
5.0/5  (39)
(39)
Find an equation of the tangent line to the graph of f at the given point.
(Multiple Choice)
4.8/5  (31)
(31)
it. The buoy moves a total of feet (vertically) between its low point and its high point. It returns to its high point every 10 seconds. Determine the velocity of the buoy as a function of .
(Multiple Choice)
4.8/5  (45)
(45)
Find the slope-intercept form of the equation of the line tangent to the graph of when
(Multiple Choice)
4.9/5  (36)
(36)
Determine all values of x, (if any), at which the graph of the function has a horizontal tangent.
(Multiple Choice)
4.9/5  (38)
(38)
Find the slope of the graph of the function at the given value. when
(Multiple Choice)
4.7/5  (38)
(38)
Complete two iterations of Newton's Method for the function
initial guess
(Multiple Choice)
4.8/5  (25)
(25)
airplane is flying in still air with an airspeed of miles per hour. If it is climbing at an angle of , find the rate at which it is gaining altitude. Round your answer to four Decimal places.
(Multiple Choice)
4.9/5  (28)
(28)
Showing 121 - 140 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)