Exam 3: The Derivative and the Tangent Line Problem
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
All edges of a cube are expanding at a rate of centimeters per second. How fast is the volume changing when each edge is centimeters?
(Multiple Choice)
4.9/5  (35)
(35)
Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two Successive approximations differ by less tha
![Newton´s Method to approximate the x-value of the indicated point of intersection of the two graphs accurate to three decimal places.Continue the process until two Successive approximations differ by less tha 0.001 \text {. [Hint: Let } h ( x ) = f ( x ) - g ( x ) . ] f ( x ) = 3 x + 1 g ( x ) = \sqrt { x + 5 }](https://storage.examlex.com/TB8682/11ecdffd_8e4b_6bf1_b7d1_73d47e42638e_TB8682_11.jpg)
(Multiple Choice)
4.9/5  (34)
(34)
a free-fall experiment, an object is dropped from a height of 256 feet. A camera on the ground 500 feet from the point of impact records the fall of the object as shown in the figure. Assuming the object is released at time . At what time will the object reach the ground level?
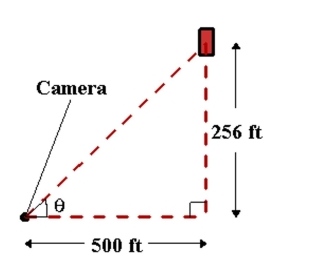
(Multiple Choice)
4.9/5  (43)
(43)
Assume that x and y are both differentiable functions of t. Find when and for the equation .
(Multiple Choice)
4.9/5  (25)
(25)
Showing 101 - 120 of 191
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)