Exam 10: Conics and Calculus
Exam 1: Graphs and Models114 Questions
Exam 2: A Preview of Calculus92 Questions
Exam 3: The Derivative and the Tangent Line Problem191 Questions
Exam 4: Extrema on an Interval147 Questions
Exam 5: Antiderivatives and Indefinite Integration167 Questions
Exam 6: Slope Fields and Eulers Method85 Questions
Exam 7: Area of a Region Between Two Curves120 Questions
Exam 8: Basic Integration Rules127 Questions
Exam 9: Sequences179 Questions
Exam 10: Conics and Calculus120 Questions
Exam 11: Vectors in the Plane125 Questions
Exam 12: Vector-Valued Functions83 Questions
Exam 13: Introduction to Functions of Several Variables124 Questions
Exam 14: Iterated Integrals and Area in the Plane118 Questions
Exam 15: Vector Fields108 Questions
Exam 16: Exact First-Order Equations45 Questions
Select questions type
Find the points of intersection of the graphs of the equations.
r= r=1.6
(Multiple Choice)
4.7/5  (37)
(37)
Classify the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.8/5  (31)
(31)
Find all points (if any) of horizontal and vertical tangency to the curve
(Multiple Choice)
4.8/5  (39)
(39)
Find a polar equation for the hyperbola with its focus at the pole, eccentricity and directrix .
(Multiple Choice)
4.8/5  (25)
(25)
Write an integral that represents the area of the shaded region for shown in the figure. Do not evaluate the integral. 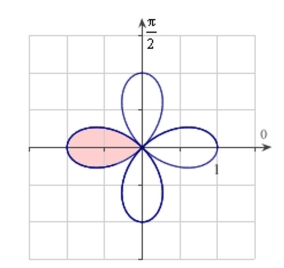
(Multiple Choice)
4.9/5  (29)
(29)
Sketch the curve represented by the parametric equations, and write the corresponding rectangular equation by eliminating the parameter. x=16+8\theta y=-4+4\theta
(Multiple Choice)
4.9/5  (40)
(40)
Find all points (if any) of horizontal and vertical tangency to the curve
(Multiple Choice)
4.9/5  (32)
(32)
Find the area of the surface formed by revolving about the polar axis the following curve over the given interval.
(Multiple Choice)
4.8/5  (34)
(34)
Uranus moves in an elliptical orbit with the sun at one of the foci. The length of the half of the major axis is 2,876,769,540 kilometers, and the eccentricity is 0.0444. Find the minimum Distance (perihelion) of Uranus from the sun. Round your answer to nearest kilometer.
(Multiple Choice)
4.9/5  (34)
(34)
Find all points (if any) of horizontal and vertical tangency to the curve
(Multiple Choice)
4.9/5  (32)
(32)
The parametric equations for the path of a projectile launched at a height h feet above the ground, at an angle with the horizontal and having an initial velocity of feet per second is given by and . The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of degrees with the horizontal at a speed of 100 miles per hour as shown in the figure. Write a set of parametric equations for the path of the ball.
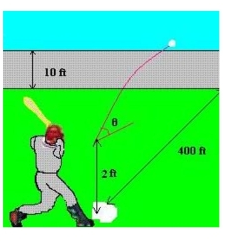
(Multiple Choice)
4.8/5  (35)
(35)
Find all points (if any) of horizontal and vertical tangency to the curve
(Multiple Choice)
4.8/5  (33)
(33)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)