Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 16: Regression Models for Nonlinear Relationships

arrow
Exam 1: Statistics and Data68 Questionsadd course
Exam 2: Tabular and Graphical Methods99 Questionsadd course
Exam 3: Numerical Descriptive Measures123 Questionsadd course
Exam 4: Basic Probability Concepts107 Questionsadd course
Exam 5: Discrete Probability Distributions118 Questionsadd course
Exam 6: Continuous Probability Distributions114 Questionsadd course
Exam 7: Sampling and Sampling Distributions110 Questionsadd course
Exam 8: Interval Estimation111 Questionsadd course
Exam 9: Hypothesis Testing111 Questionsadd course
Exam 10: Statistical Inference Concerning Two Populations104 Questionsadd course
Exam 11: Statistical Inference Concerning Variance96 Questionsadd course
Exam 12: Chi-Square Tests100 Questionsadd course
Exam 13: Analysis of Variance89 Questionsadd course
Exam 14: Regression Analysis116 Questionsadd course
Exam 15: Inference With Regression Models117 Questionsadd course
Exam 16: Regression Models for Nonlinear Relationships95 Questionsadd course
Exam 17: Regression Models With Dummy Variables117 Questionsadd course
Exam 18: Time Series and Forecasting103 Questionsadd course
Exam 19: Returns, Index Numbers and Inflation98 Questionsadd course
Exam 20: Nonparametric Tests99 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

The coefficient of determination R2 cannot be used to compare the linear and quadratic models,because:

(Multiple Choice)
4.8/5
(28)
Question 61

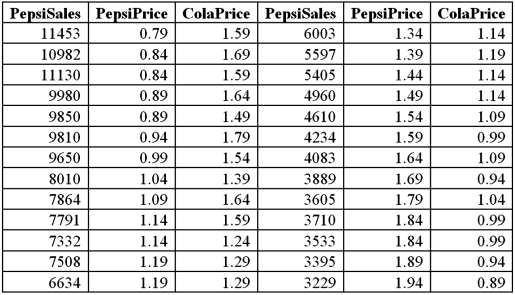Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(PepsiPrice). Using Excel's regression,the linear model PepsiSales = β0 + β1PepsiPrice + β2ColaPrice + ε and the log-log model ln(PepsiSales)= β0 + β1ln(PepsiPrice)+ β2ln(ColaPrice)+ ε have been estimated as follows: 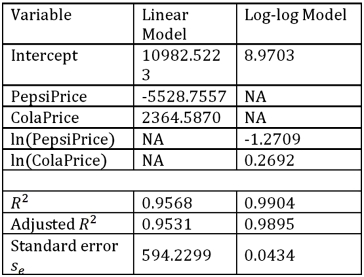Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(PepsiPrice). Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(PepsiPrice).

(Essay)
4.8/5
(36)
Question 62

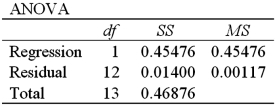
Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.How many minutes must elapse after the brewing in order to cool the coffee to 158 <sup>o</sup>F? For the assumed exponential model ln(Temp)= β0 + β1Time + ε,the following Excel regression partial output is available. Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.How many minutes must elapse after the brewing in order to cool the coffee to 158 <sup>o</sup>F? Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.How many minutes must elapse after the brewing in order to cool the coffee to 158 <sup>o</sup>F? Refer to Exhibit 16-4.How many minutes must elapse after the brewing in order to cool the coffee to 158 oF?

(Multiple Choice)
4.8/5
(28)
Question 63

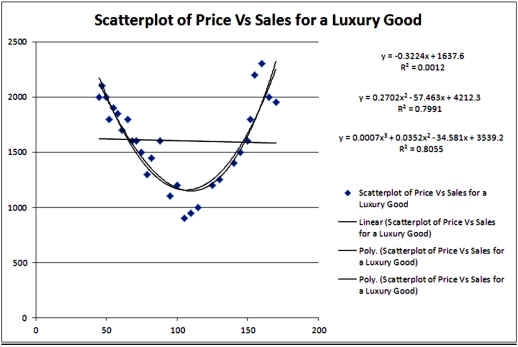Exhibit 16.2.Typically,the sales volume declines with an increase of a product price.It has been observed,however,that for some luxury goods the sales volume may increase when the price increases.The following Excel output illustrates this rather unusual relationship. Exhibit 16.2.Typically,the sales volume declines with an increase of a product price.It has been observed,however,that for some luxury goods the sales volume may increase when the price increases.The following Excel output illustrates this rather unusual relationship. Refer to Exhibit 16.2.For the considered range of the price,the relationship between Price and Sales should be described by a: Refer to Exhibit 16.2.For the considered range of the price,the relationship between Price and Sales should be described by a:

(Multiple Choice)
4.8/5
(37)
Question 64

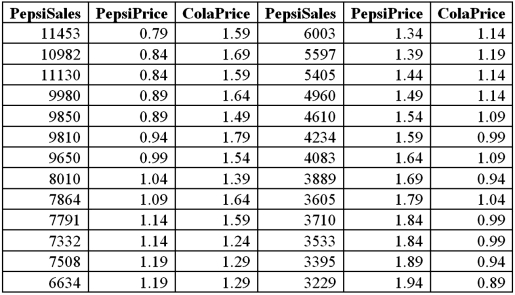Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(ColaPrice). Using Excel's regression,the linear model PepsiSales = β0 + β1PepsiPrice + β2ColaPrice + ε and the log-log model ln(PepsiSales)= β0 + β1ln(PepsiPrice)+ β2ln(ColaPrice)+ ε have been estimated as follows: 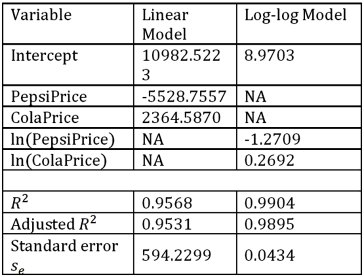Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(ColaPrice). Refer to Exhibit 16.7.For the estimated log-log model,interpret the estimated coefficient of ln(ColaPrice).

(Essay)
4.9/5
(36)
Question 65

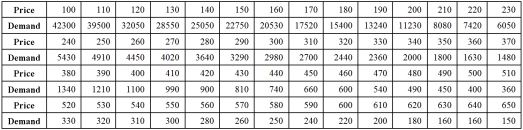Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.Using the cubic model,what is the predicted demand when the price is $200? For the assumed cubic and log-log regression models,Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand)= β0 + β1ln(Price)+ ε,the following regression results are available: 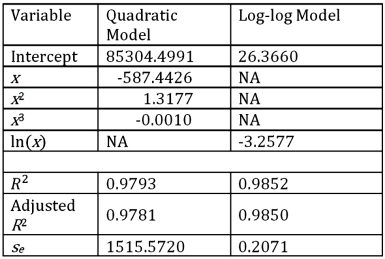Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.Using the cubic model,what is the predicted demand when the price is $200? Refer to Exhibit 16.5.Using the cubic model,what is the predicted demand when the price is $200?

(Multiple Choice)
4.8/5
(44)
Question 66

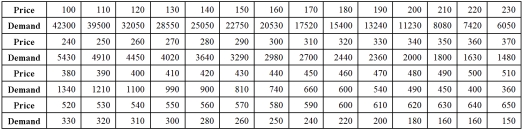Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.Assuming that the sample correlation coefficient between Demand and is 0.956,what is the predicted demand for a price of $250 found by the model with better fit? 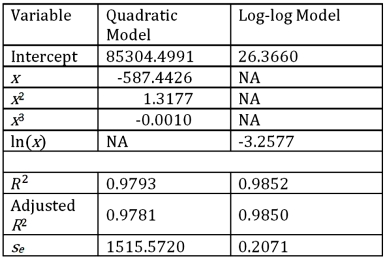For the assumed cubic and log-log regression models,Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand)= β0 + β1ln(Price)+ ε,the following regression results are available: Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.Assuming that the sample correlation coefficient between Demand and is 0.956,what is the predicted demand for a price of $250 found by the model with better fit? 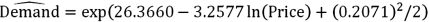Refer to Exhibit 16.5.Assuming that the sample correlation coefficient between Demand and Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.Assuming that the sample correlation coefficient between Demand and is 0.956,what is the predicted demand for a price of $250 found by the model with better fit? is 0.956,what is the predicted demand for a price of $250 found by the model with better fit?

(Multiple Choice)
4.8/5
(31)
Question 67

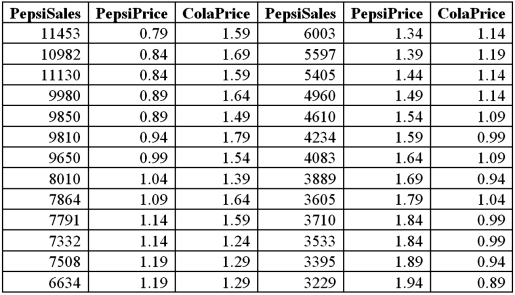Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.What is the percentage of variations in the sales of Pepsi explained by the estimated linear model? Using Excel's regression,the linear model PepsiSales = β0 + β1PepsiPrice + β2ColaPrice + ε and the log-log model ln(PepsiSales)= β0 + β1ln(PepsiPrice)+ β2ln(ColaPrice)+ ε have been estimated as follows: 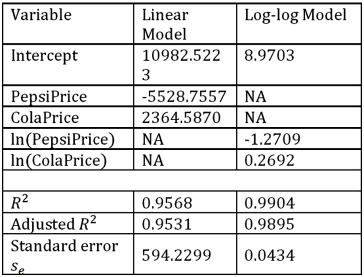Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.What is the percentage of variations in the sales of Pepsi explained by the estimated linear model? Refer to Exhibit 16.7.What is the percentage of variations in the sales of Pepsi explained by the estimated linear model?

(Short Answer)
4.8/5
(49)
Question 68

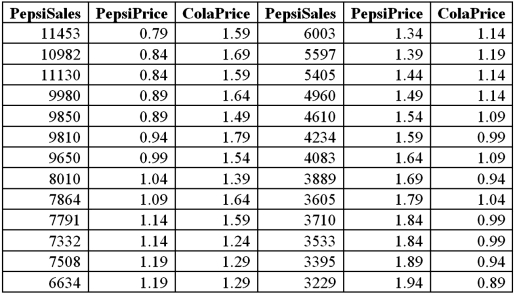Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated linear model,when the price of Cola is held constant what is the predicted change in the Pepsi sales if the price of Pepsi increases by 10 cents? Using Excel's regression,the linear model PepsiSales = β0 + β1PepsiPrice + β2ColaPrice + ε and the log-log model ln(PepsiSales)= β0 + β1ln(PepsiPrice)+ β2ln(ColaPrice)+ ε have been estimated as follows: 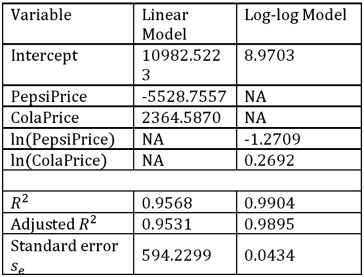Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.For the estimated linear model,when the price of Cola is held constant what is the predicted change in the Pepsi sales if the price of Pepsi increases by 10 cents? Refer to Exhibit 16.7.For the estimated linear model,when the price of Cola is held constant what is the predicted change in the Pepsi sales if the price of Pepsi increases by 10 cents?

(Essay)
4.8/5
(35)
Question 69

Exhibit 16-1.The following Excel scatterplot with the fitted quadratic regression equation illustrates the observed relationship between productivity and the number of hired workers. Exhibit 16-1.The following Excel scatterplot with the fitted quadratic regression equation illustrates the observed relationship between productivity and the number of hired workers. 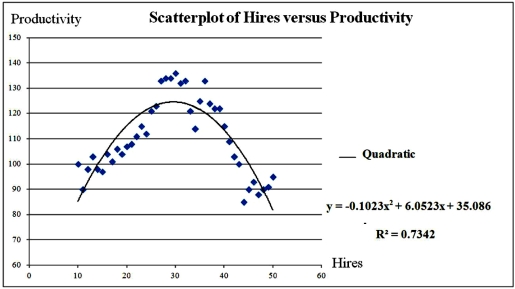Refer to Exhibit 16.1.Assuming that the number of hired workers must be integer,how many workers should be hired in order to achieve the highest productivity? Refer to Exhibit 16.1.Assuming that the number of hired workers must be integer,how many workers should be hired in order to achieve the highest productivity?

(Multiple Choice)
4.9/5
(35)
Question 70

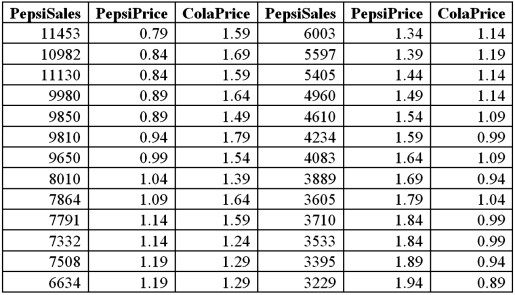Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.Discuss the choice between the linear model and the log-log model. Using Excel's regression,the linear model PepsiSales = β0 + β1PepsiPrice + β2ColaPrice + ε and the log-log model ln(PepsiSales)= β0 + β1ln(PepsiPrice)+ β2ln(ColaPrice)+ ε have been estimated as follows: 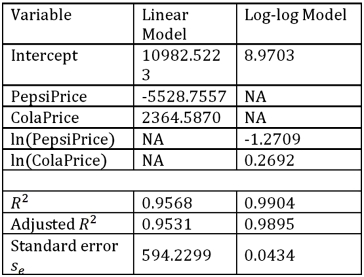Exhibit 16-7.It is believed that the sales volume of one liter Pepsi bottles depends on the price of the bottle and the price of one liter bottle of Coca Cola.The following data has been collected for a certain sales region. Using Excel's regression,the linear model PepsiSales = β<sub>0</sub> + β<sub>1</sub>PepsiPrice + β<sub>2</sub>ColaPrice + ε and the log-log model ln(PepsiSales)= β<sub>0</sub> + β<sub>1</sub>ln(PepsiPrice)+ β<sub>2</sub>ln(ColaPrice)+ ε have been estimated as follows: Refer to Exhibit 16.7.Discuss the choice between the linear model and the log-log model. Refer to Exhibit 16.7.Discuss the choice between the linear model and the log-log model.

(Essay)
5.0/5
(29)
Question 71

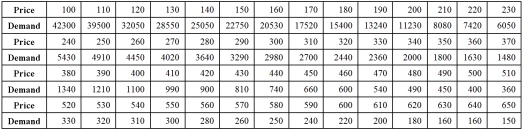Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.What is the percentage of variations in ln(Demand)explained by the log-log regression equation? For the assumed cubic and log-log regression models,Demand = β0 + β1Price + β2Price2 + β3Price3 + ε and ln(Demand)= β0 + β1ln(Price)+ ε,the following regression results are available: 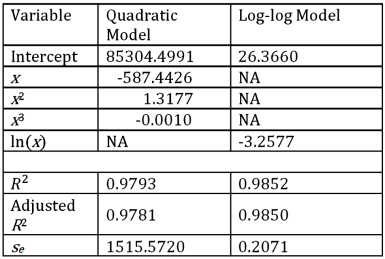Exhibit 16.5.The following data shows the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models,Demand = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Price<sup>2</sup> + β<sub>3</sub>Price<sup>3</sup> + ε and ln(Demand)= β<sub>0</sub> + β<sub>1</sub>ln(Price)+ ε,the following regression results are available: Refer to Exhibit 16.5.What is the percentage of variations in ln(Demand)explained by the log-log regression equation? Refer to Exhibit 16.5.What is the percentage of variations in ln(Demand)explained by the log-log regression equation?

(Multiple Choice)
4.7/5
(36)
Question 72

A quadratic regression model is a special type of a polynomial regression model.

(True/False)
4.9/5
(36)
Question 73

For the quadratic equation For the quadratic equation 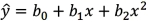,which of the following expressions must be zero in order to minimize or maximize the predicted y? ,which of the following expressions must be zero in order to minimize or maximize the predicted y?

(Multiple Choice)
4.9/5
(33)
Question 74

Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.What is the regression equation for making predictions concerning the coffee temperature? For the assumed exponential model ln(Temp)= β0 + β1Time + ε,the following Excel regression partial output is available. Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.What is the regression equation for making predictions concerning the coffee temperature? Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. 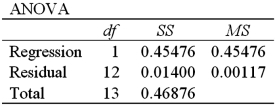Refer to Exhibit 16-4.What is the regression equation for making predictions concerning the coffee temperature? Refer to Exhibit 16-4.What is the regression equation for making predictions concerning the coffee temperature?

(Multiple Choice)
4.9/5
(36)
Question 75

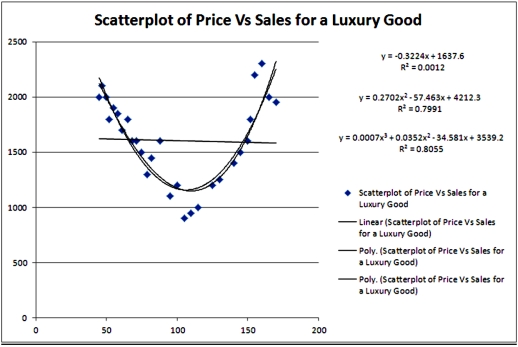Exhibit 16.2.Typically,the sales volume declines with an increase of a product price.It has been observed,however,that for some luxury goods the sales volume may increase when the price increases.The following Excel output illustrates this rather unusual relationship. Exhibit 16.2.Typically,the sales volume declines with an increase of a product price.It has been observed,however,that for some luxury goods the sales volume may increase when the price increases.The following Excel output illustrates this rather unusual relationship. Refer to Exhibit 16.2.What can be said about the linear relationship between Price and Sales? Refer to Exhibit 16.2.What can be said about the linear relationship between Price and Sales?

(Multiple Choice)
4.7/5
(38)
Question 76

When the data is available on x and y,it is easy to estimate a polynomial regression model.

(True/False)
4.8/5
(40)
Question 77

The fit of the models y = β0 + β1x + β2x2 + ε and y = β0 + β1ln(x)+ ε can be compared using the coefficient of determination R2.

(True/False)
4.8/5
(27)
Question 78

The cubic regression model,y = β0 + β1x + β2x2+ β3x3 + ε,is used when we assume that the relationship between x and y should be captured by a function that has either minimum or maximum,but not both.

(True/False)
4.9/5
(32)
Question 79

Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.What is the standard error of the estimate? For the assumed exponential model ln(Temp)= β0 + β1Time + ε,the following Excel regression partial output is available. Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. Refer to Exhibit 16-4.What is the standard error of the estimate? Exhibit 16-4.The following data shows the cooling temperatures of a freshly brewed cup of coffee after it is poured from the brewing pot into a serving cup.The brewing pot temperature is approximately 180º F;see http://mathbits.com/mathbits/tisection/statistics2/exponential.htm For the assumed exponential model ln(Temp)= β<sub>0</sub> + β<sub>1</sub>Time + ε,the following Excel regression partial output is available. 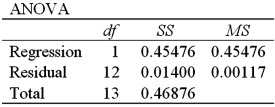Refer to Exhibit 16-4.What is the standard error of the estimate? Refer to Exhibit 16-4.What is the standard error of the estimate?

(Multiple Choice)
4.8/5
(32)
Question 80
Showing 61 - 80 of 95
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)