Exam 13: Multiple Regression Analysis
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
A multiple regression model involves 5 predictor variables and 30 observations. If we want to test the hypotheses 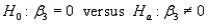 at the 5% significance level, what will the critical value of the rejection region be?
at the 5% significance level, what will the critical value of the rejection region be?
(Multiple Choice)
4.8/5  (33)
(33)
College Textbook Sales Narrative
A publisher of college textbooks conducted a study to relate profit per text y to cost of sales x over a six-year period when its sales force (and sales costs) were growing rapidly. These inflation-adjusted data (in thousands of dollars) were collected:  Expecting profit per book to rise and then plateau, the publisher fitted the model
Expecting profit per book to rise and then plateau, the publisher fitted the model 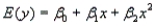 to the data.
-Refer to College Textbook Sales Narrative. Find s on the printout. Confirm that
to the data.
-Refer to College Textbook Sales Narrative. Find s on the printout. Confirm that 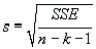 .
.
(Essay)
4.9/5  (33)
(33)
Personal Spending and Personal Income
Is personal spending linearly related to orders for durable goods and personal income? A recent study reported the amounts of personal spending (in trillions of dollars), amount spent on durable goods (in billions of dollars), and personal income (in trillions of dollars). A statistical package was used to fit a linear regression model, producing the output below. 
 R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Use the computer output shown above to calculate 95% confidence intervals for the intercept and the partial regression coefficients.
R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Use the computer output shown above to calculate 95% confidence intervals for the intercept and the partial regression coefficients.
(Essay)
4.9/5  (32)
(32)
In multiple regression, the descriptor "multiple" refers to more than one dependent variable.
(True/False)
4.7/5  (39)
(39)
In multiple regression analysis, when the response surface (the graphical depiction of the regression equation) hits every single point, the sum of squares for error SSE = 0, the standard error of estimate 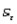 = 0, and the coefficient of determination
= 0, and the coefficient of determination 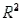 = 1.
= 1.
(True/False)
4.8/5  (33)
(33)
Personal Spending and Personal Income
Is personal spending linearly related to orders for durable goods and personal income? A recent study reported the amounts of personal spending (in trillions of dollars), amount spent on durable goods (in billions of dollars), and personal income (in trillions of dollars). A statistical package was used to fit a linear regression model, producing the output below. 
 R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Based on your confidence intervals in the previous question, does the amount spent on durable goods have any predictive power beyond that provided by the other independent variables for determining personal spending? Explain.
R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Based on your confidence intervals in the previous question, does the amount spent on durable goods have any predictive power beyond that provided by the other independent variables for determining personal spending? Explain.
(Essay)
4.9/5  (39)
(39)
Life Expectancy Narrative
An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death (y), the average number of hours of exercise per week ( 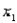 ), the cholesterol level (
), the cholesterol level ( 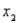 ), and the number of points that the individual's blood pressure exceeded the recommended value (
), and the number of points that the individual's blood pressure exceeded the recommended value ( 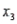 ). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below.
The regression equation is
). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below.
The regression equation is 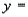
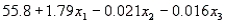
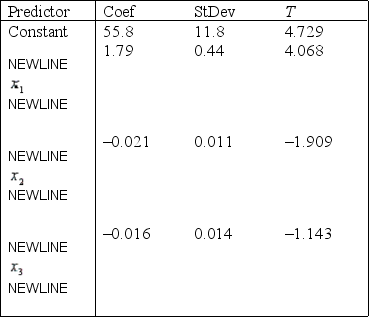 S = 9.47 R-Sq = 22.5%
Analysis of Variance
S = 9.47 R-Sq = 22.5%
Analysis of Variance 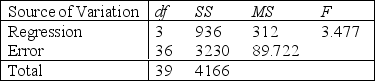 -Refer to Life Expectancy Narrative. Interpret the coefficient
-Refer to Life Expectancy Narrative. Interpret the coefficient 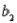 .
.
(Essay)
4.9/5  (30)
(30)
In multiple regression analysis, the coefficient of determination is sometimes called multiple  .
.
(True/False)
4.8/5  (31)
(31)
The coefficient of multiple determination is calculated by dividing the regression sum of squares by the total sum of squares (SSR/SST) and subtracting that value from 1.
(True/False)
5.0/5  (37)
(37)
Life Expectancy Narrative
An actuary wanted to develop a model to predict how long individuals will live. After consulting a number of physicians, she collected the age at death (y), the average number of hours of exercise per week ( 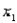 ), the cholesterol level (
), the cholesterol level ( 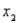 ), and the number of points that the individual's blood pressure exceeded the recommended value (
), and the number of points that the individual's blood pressure exceeded the recommended value ( 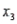 ). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below.
The regression equation is
). A random sample of 40 individuals was selected. The computer output of the multiple regression model is shown below.
The regression equation is 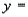
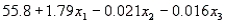
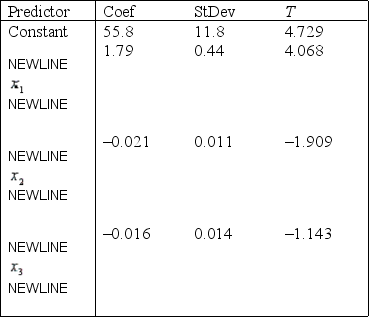 S = 9.47 R-Sq = 22.5%
Analysis of Variance
S = 9.47 R-Sq = 22.5%
Analysis of Variance  -Refer to Life Expectancy Narrative. Is there enough evidence at the 5% significance level to infer that the cholesterol level and the age at death are negatively linearly related? Justify your conclusion.
-Refer to Life Expectancy Narrative. Is there enough evidence at the 5% significance level to infer that the cholesterol level and the age at death are negatively linearly related? Justify your conclusion.
(Essay)
4.8/5  (33)
(33)
If we want to relate a random variable y to two independent variables 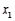 and
and 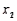 , a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs.
, a regression hyperplane is the three-dimensional equivalent of a regression line that minimizes the sum of the squared vertical deviations between the sample points suspended in y vs. 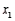 vs.
vs. 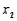 space and their associated multiple regression estimates, all of which lie on this hyperplane.
space and their associated multiple regression estimates, all of which lie on this hyperplane.
(True/False)
4.9/5  (28)
(28)
Demographic Variables and TV Narrative
A statistician wanted to determine if the demographic variables of age, education, and income influence the number of hours of television watched per week. A random sample of 25 adults was selected to estimate the multiple regression model: 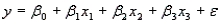 , where y is the number of hours of television watched last week,
, where y is the number of hours of television watched last week, 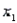 is the age (in years),
is the age (in years), 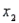 is the number of years of education, and
is the number of years of education, and 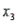 is income (in $1000s). The computer output is shown below.
The regression equation is
is income (in $1000s). The computer output is shown below.
The regression equation is 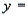
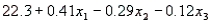
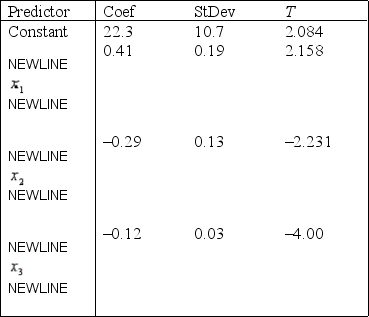 S = 4.51 R-Sq = 34.8%
Analysis of Variance
S = 4.51 R-Sq = 34.8%
Analysis of Variance 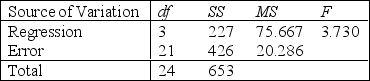 -Refer to Demographic Variables and TV Narrative. Is there sufficient evidence at the 1% significance level to indicate that hours of television watched and education are negatively linearly related? Justify your conclusion.
-Refer to Demographic Variables and TV Narrative. Is there sufficient evidence at the 1% significance level to indicate that hours of television watched and education are negatively linearly related? Justify your conclusion.
(Essay)
4.7/5  (26)
(26)
Chemical Comparisons Narrative
A chemist was interested in examining the effects of three chemicals on a chemical process yield. Let 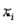 , i = 1, 2, 3, represent the effects of the three chemicals, respectively, and y be the process yield. The following output was generated using statistical software.
Regression Analysis
, i = 1, 2, 3, represent the effects of the three chemicals, respectively, and y be the process yield. The following output was generated using statistical software.
Regression Analysis  S = 14.01 R-Sq = 95.1% R-Sq(adj) = 92.1
Analysis of Variance
S = 14.01 R-Sq = 95.1% R-Sq(adj) = 92.1
Analysis of Variance  -Refer to Chemical Comparisons Narrative. Which variable, if any, should be removed from the model if a 0.05 level of significance is desired?
-Refer to Chemical Comparisons Narrative. Which variable, if any, should be removed from the model if a 0.05 level of significance is desired?
(Essay)
4.9/5  (27)
(27)
For which of the following quantities is the adjusted multiple coefficient of determination adjusted??
(Multiple Choice)
4.9/5  (38)
(38)
College Textbook Sales Narrative
A publisher of college textbooks conducted a study to relate profit per text y to cost of sales x over a six-year period when its sales force (and sales costs) were growing rapidly. These inflation-adjusted data (in thousands of dollars) were collected:  Expecting profit per book to rise and then plateau, the publisher fitted the model
Expecting profit per book to rise and then plateau, the publisher fitted the model 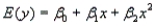 to the data.
-Refer to College Textbook Sales Narrative. Do the data provide sufficient evidence to indicate that the model contributes information for the prediction of y? What is the p-value for this test, and what does it mean?
to the data.
-Refer to College Textbook Sales Narrative. Do the data provide sufficient evidence to indicate that the model contributes information for the prediction of y? What is the p-value for this test, and what does it mean?
(Essay)
4.8/5  (35)
(35)
If a multiple regression model includes ten or more predictor variables, it is almost certain that changes in the predictor variables cause changes in the response variable y.
(True/False)
4.9/5  (34)
(34)
Personal Spending and Personal Income
Is personal spending linearly related to orders for durable goods and personal income? A recent study reported the amounts of personal spending (in trillions of dollars), amount spent on durable goods (in billions of dollars), and personal income (in trillions of dollars). A statistical package was used to fit a linear regression model, producing the output below. 
 R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Predict the level of personal spending when amount spent on durable goods is 130 and personal income is at 5.10.
R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Predict the level of personal spending when amount spent on durable goods is 130 and personal income is at 5.10.
(Essay)
4.9/5  (37)
(37)
Personal Spending and Personal Income
Is personal spending linearly related to orders for durable goods and personal income? A recent study reported the amounts of personal spending (in trillions of dollars), amount spent on durable goods (in billions of dollars), and personal income (in trillions of dollars). A statistical package was used to fit a linear regression model, producing the output below. 
 R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Use the computer output shown above to test the hypotheses
R2 = 95.9% R2(adj) = 95.0%, s = 0.0144 with 12 - 3 = 9 df.
-Refer to Personal Spending and Personal Income. Use the computer output shown above to test the hypotheses 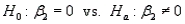 at the 5% significance level. What is your conclusion?
at the 5% significance level. What is your conclusion?
(Essay)
4.8/5  (34)
(34)
Which of the following correctly describes the coefficient of multiple determination?
(Multiple Choice)
4.7/5  (34)
(34)
In stepwise regression procedure, what occurs if two independent variables are highly correlated?
(Multiple Choice)
4.8/5  (33)
(33)
Showing 21 - 40 of 232
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)