Exam 15: Random Variables
Exam 1: Data30 Questions
Exam 2: Displaying and Describing Categorical Data65 Questions
Exam 3: Displaying and Summarizing Quantitative Data93 Questions
Exam 4: Understanding and Comparing Distributions102 Questions
Exam 5: The Standard Deviation As a Ruler and the Normal Model131 Questions
Exam 6: Scatterplots, association, and Correlation74 Questions
Exam 7: Linear Regression57 Questions
Exam 8: Regression Wisdom32 Questions
Exam 9: Re-Expressing Data: Get It Straight51 Questions
Exam 10: Understanding Randomness26 Questions
Exam 11: Sample Surveys50 Questions
Exam 12: Experiments and Observational Surveys87 Questions
Exam 13: From Randomness to Probability64 Questions
Exam 14: Probability Rules90 Questions
Exam 15: Random Variables112 Questions
Exam 16: Probability Models114 Questions
Exam 17: Sampling Distribution Models45 Questions
Exam 18: Confidence Intervals for Proportions56 Questions
Exam 19: Testing Hypotheses About Proportions50 Questions
Exam 20: More About Tests69 Questions
Exam 21: Comparing Two Proportions52 Questions
Exam 22: Inferences About Means106 Questions
Exam 23: Comparing Means43 Questions
Exam 24: Paired Samples and Blocks33 Questions
Exam 25: Comparing Counts78 Questions
Exam 26: Inferences for Regression51 Questions
Exam 27: Analysis of Variance39 Questions
Exam 28: Multifactor Analysis of Variance22 Questions
Exam 29: Multiple Regression22 Questions
Exam 30: Multiple Regression Wisdom21 Questions
Exam 31: Rank-Based Nonparametric Tests29 Questions
Exam 32: The Bootstrap31 Questions
Select questions type
The probability model below describes the number of thunderstorms that a certain town may experience during the month of August. 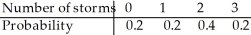 How many storms can the town expect each August?
How many storms can the town expect each August?
Free
(Multiple Choice)
4.8/5  (39)
(39)
Correct Answer:
E
You pick a card from a deck.If you get a face card,you win $5.If you get an ace,you win $30 plus an extra $50 for the ace of hearts.For any other card you win nothing.
Create a probability model for the amount you win at this game.
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
B
The amount of money that Maria earns in a week is a random variable,X,with a mean of $800 and a standard deviation of $20.The amount of money that Daniel earns in a week is a random variable,Y,with a mean of $900 and a standard deviation of $30.
The total,X +Y,of Maria's weekly income and Daniel's weekly income is a random variable with a mean of $800 + $900 = $1700 and a standard deviation of 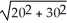 ≈ $36.
The calculation of the standard deviation requires the assumption that the incomes are independent of one another.Which of the following examples describes a situation in which that assumption may be violated?
A: Maria and Daniel are married to each other
B: Maria and Daniel work for the same company
C: Maria and Daniel work in the same business
D: Maria and Daniel were born in the same year
≈ $36.
The calculation of the standard deviation requires the assumption that the incomes are independent of one another.Which of the following examples describes a situation in which that assumption may be violated?
A: Maria and Daniel are married to each other
B: Maria and Daniel work for the same company
C: Maria and Daniel work in the same business
D: Maria and Daniel were born in the same year
(Multiple Choice)
4.9/5  (34)
(34)
You have arranged to go camping for two days in March.You believe that the probability that it will rain on the first day is 0.3.If it rains on the first day,the probability that it also rains on the second day is 0.5.If it doesn't rain on the first day,the probability that it rains on the second day is 0.3.Let the random variable X be the number of rainy days during your camping trip.Find the probability model for X.
(Multiple Choice)
4.8/5  (35)
(35)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable 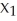 +
+ 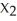 +
+ 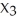 .
. 
(Multiple Choice)
4.9/5  (36)
(36)
The amount of money that Jon can save after working for a summer is a random variable S with a mean of $1,500 and a standard deviation of $100.After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of 17,500 Rupees and a standard deviation of 600 Rupees.The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P which can be expressed in terms of S and B as P = 43S - B.Find the mean and standard deviation of P in Rupees.Assume that Jon's savings and the price of the bike are independent.
(Multiple Choice)
4.8/5  (43)
(43)
Sue buys a large packet of rice.The amount of rice that the manufacturer puts in the packet is a random variable with a mean of 1,022 g and a standard deviation of 11 g.The amount of rice that Sue uses in a week has a mean of 240 g and a standard deviation of 26 g.Find the mean and standard deviation of the amount of rice remaining in the packet after a week.
(Multiple Choice)
4.9/5  (33)
(33)
In a box of 7 batteries,3 are dead.You choose two batteries at random from the box.Let the random variable X be the number of good batteries you get.Find the probability model for X.
(Multiple Choice)
4.8/5  (39)
(39)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable 0.3Y. 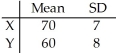
(Multiple Choice)
4.8/5  (36)
(36)
The amount of money that Jon can save after working for a summer is a random variable S with a mean of $1,700 and a standard deviation of $100.After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of 18,500 Rupees and a standard deviation of 500 Rupees.The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P.Write an expression for P in terms of S and B.
(Multiple Choice)
4.8/5  (33)
(33)
The accompanying table describes the probability distribution for the number of adults in a certain town (among 4 randomly selected adults)who have a college degree. 
(Multiple Choice)
4.9/5  (36)
(36)
You pick a card from a deck.If you get a club,you win $80.If not,you get to draw again (after replacing the first card).If you get a club the second time,you win $30.If not,you lose.Find the standard deviation of the amount you will win.
(Multiple Choice)
4.9/5  (38)
(38)
Suppose that in one town,50-year old men have a mean weight of 80 kg with a standard deviation of 7 kg.30-year old men have a mean weight of 71 kg with a standard deviation of 6 kg.How much heavier do you expect a 50-year old man to be than a 30-year old man and what is the standard deviation of this difference?
(Multiple Choice)
4.9/5  (28)
(28)
The amount of cereal that a manufacturer puts in its boxes of cereal is a random variable with a mean of 1,020 g and a standard deviation of 10 g.The amount of cereal that Tyler eats for breakfast is a random variable with a mean of 65 g and a standard deviation of 6 g.The amount of cereal that Tyler's wife,Suzanne,eats for breakfast is a random variable with a mean of 53 g and a standard deviation of 2 g.If Tyler and Suzanne open a new packet of cereal one Monday morning,find the mean and standard deviation of the amount of cereal remaining in the packet after one breakfast.Assume that the amount that Tyler eats is independent of the amount Suzanne eats.
(Multiple Choice)
5.0/5  (34)
(34)
The number of emergency calls received by a switchboard in an hour has an expected value of 0.5 and a standard deviation of 0.7.Find the mean and standard deviation of the number of emergency calls received by the switch board during a workshift lasting 4 hours.Assume that the hours are independent of each other.
(Multiple Choice)
4.9/5  (28)
(28)
Showing 1 - 20 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)