Exam 15: Random Variables
Exam 1: Data30 Questions
Exam 2: Displaying and Describing Categorical Data65 Questions
Exam 3: Displaying and Summarizing Quantitative Data93 Questions
Exam 4: Understanding and Comparing Distributions102 Questions
Exam 5: The Standard Deviation As a Ruler and the Normal Model131 Questions
Exam 6: Scatterplots, association, and Correlation74 Questions
Exam 7: Linear Regression57 Questions
Exam 8: Regression Wisdom32 Questions
Exam 9: Re-Expressing Data: Get It Straight51 Questions
Exam 10: Understanding Randomness26 Questions
Exam 11: Sample Surveys50 Questions
Exam 12: Experiments and Observational Surveys87 Questions
Exam 13: From Randomness to Probability64 Questions
Exam 14: Probability Rules90 Questions
Exam 15: Random Variables112 Questions
Exam 16: Probability Models114 Questions
Exam 17: Sampling Distribution Models45 Questions
Exam 18: Confidence Intervals for Proportions56 Questions
Exam 19: Testing Hypotheses About Proportions50 Questions
Exam 20: More About Tests69 Questions
Exam 21: Comparing Two Proportions52 Questions
Exam 22: Inferences About Means106 Questions
Exam 23: Comparing Means43 Questions
Exam 24: Paired Samples and Blocks33 Questions
Exam 25: Comparing Counts78 Questions
Exam 26: Inferences for Regression51 Questions
Exam 27: Analysis of Variance39 Questions
Exam 28: Multifactor Analysis of Variance22 Questions
Exam 29: Multiple Regression22 Questions
Exam 30: Multiple Regression Wisdom21 Questions
Exam 31: Rank-Based Nonparametric Tests29 Questions
Exam 32: The Bootstrap31 Questions
Select questions type
An insurance company estimates that it should make an annual profit of $150 on each homeowner's policy written,with a standard deviation of $6,000.If it writes 7 of these policies,what are the mean and standard deviation of the annual profit? Assume that policies are independent of each other.
(Multiple Choice)
4.8/5  (36)
(36)
A police department reports that the probabilities that 0,1,2,and 3 burglaries will be reported in a given day are 0.52,0.42,0.05,and 0.01,respectively.Find the standard deviation of the number of burglaries in a day.
(Multiple Choice)
4.9/5  (37)
(37)
A couple plans to have children until they get a boy,but they agree that they will not have more than four children even if all are girls.
Create a probability model for the number of children they will have.Assume that boys and girls are equally likely.
(Multiple Choice)
4.9/5  (32)
(32)
An insurance company estimates that it should make an annual profit of $150 on each homeowner's policy written,with a standard deviation of $6000.If it writes three of these policies,the mean annual profit for the company is found to be 3 × 150 = 450.The standard deviation of the company's annual profit is found to be 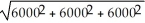 ≈ $10,392.
The calculation of the standard deviation requires the assumption that the policies are independent of one another.Which of the following examples describes a situation in which that assumption may be violated?
A: The houses are close to each other and may all be affected by the same catastrophe such as earthquake,flooding,or fire.
B: The owners all bought their homes in the same year and may all be affected by a downturn in the market
C: The owners of the three homes are related
D: All three houses were bought for the same price
≈ $10,392.
The calculation of the standard deviation requires the assumption that the policies are independent of one another.Which of the following examples describes a situation in which that assumption may be violated?
A: The houses are close to each other and may all be affected by the same catastrophe such as earthquake,flooding,or fire.
B: The owners all bought their homes in the same year and may all be affected by a downturn in the market
C: The owners of the three homes are related
D: All three houses were bought for the same price
(Multiple Choice)
4.9/5  (33)
(33)
You pick a card from a deck.If you get a club,you win $90.If not,you get to draw again (after replacing the first card).If you get a club the second time,you win $30.If not,you lose.
Find the expected amount you will win.
(Multiple Choice)
4.7/5  (27)
(27)
A slot machine at a casino pays out an average of $0.93,with a standard deviation of $120.It costs a dollar to play.If a person plays 10 times,what are the mean and standard deviation of the casino's profit?
(Multiple Choice)
4.8/5  (33)
(33)
A carnival game offers a $120 cash prize for anyone who can break a balloon by throwing a dart at it.It costs $9 to play and you're willing to spend up to $36 trying to win.You estimate that you have a 10% chance of hitting the balloon on any throw.Find the expected amount you will win.Assume that throws are independent of each other.
(Multiple Choice)
5.0/5  (34)
(34)
Miguel buys a large bottle and a small bottle of juice.The amount of juice that the manufacturer puts in the large bottle is a random variable with a mean of 1,024 ml and a standard deviation of 12 ml.The amount of juice that the manufacturer puts in the small bottle is a random variable with a mean of 504 ml and a standard deviation of 2 ml.If the total amount of juice in the two bottles can be described by a normal model,what's the probability that the total amount of juice in the two bottles is more than 1,554.8 ml?
(Multiple Choice)
4.8/5  (18)
(18)
The amount of money that Maria earns in a week is a random variable with a mean of $930 and a standard deviation of $30.The amount of money that Elena earns in a week is a random variable with a mean of $780 and a standard deviation of $15.If the difference between Maria's weekly income and Elena's weekly income can be described be a Normal model,what is the probability that Maria's weekly income is at least $223.79 more than Elena's weekly income? (In other words,what is the probability that the difference M - E is at least $223.79?)Assume that Maria's earnings are independent of Elena's earnings.
(Multiple Choice)
4.7/5  (27)
(27)
If X and Y are independent random variables then the standard deviation of the random variable X - Y is given by which of the following expressions?
(Multiple Choice)
4.8/5  (36)
(36)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable X + 6.Round to two decimal places if necessary. 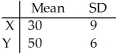
(Multiple Choice)
4.9/5  (33)
(33)
Find the standard deviation for the given probability distribution. 
(Multiple Choice)
4.9/5  (46)
(46)
You roll a pair of dice.If you get a sum greater than 10 you win $60.If you get a double you win $20.If you get a double and a sum greater than 10 you win $80.Otherwise you win nothing.You pay $5 to play.Find the expected amount you win at this game.
(Multiple Choice)
4.8/5  (35)
(35)
The probabilities that a batch of 4 computers will contain 0,1,2,3,and 4 defective computers are 0.4096,0.4096,0.1536,0.0256,and 0.0016,respectively.Find the expected number of defective computers in a batch of 4.
(Multiple Choice)
4.8/5  (34)
(34)
Hugh buys $8,000 worth of stock in an electronics company which he hopes to sell afterward at a profit.The company is developing a new laptop computer and a new desktop computer.If it releases both computers before its competitor,the value of Hugh's stock will jump to $21,000.If it releases one of the computers before its competitor,the value of Hugh's stock will jump to $17,000.If it fails to release either computer before its competitor,Hugh's stock will be worth only $5,000.Hugh believes that there is a 40% chance that the company will release the laptop before its competitor and a 50% chance that the company will release the desktop before its competitor.Create a probability model for Hugh's profit.Assume that the development of the laptop and the development of the desktop are independent events.
(Multiple Choice)
4.7/5  (35)
(35)
A company is interviewing applicants for managerial positions.They plan to hire two people.They have already rejected most candidates and are left with a group of 7 applicants of whom 6 are women.Unable to differentiate further between the applicants,they choose two people at random from this group of 7.Let the random variable X be the number of men that are chosen.Find the standard deviation of X.
(Multiple Choice)
4.8/5  (34)
(34)
You roll a pair of dice.If you get a sum greater than 10 you win $50.If you get a double you win $20.If you get a double and a sum greater than 10 you win a $70.Otherwise you win nothing.Find the standard deviation of the amount you win at this game.
(Multiple Choice)
4.8/5  (32)
(32)
You roll a fair die.If you get a number greater than 4,you win $70.If not,you get to roll again.If you get a number greater then 4 the second time,you win $30.Otherwise you win nothing.
Create a probability model for the amount you win at this game.
(Multiple Choice)
4.7/5  (30)
(30)
An insurance policy costs $150 per year,and will pay policyholders $16,000 if they suffer a major injury (resulting in hospitalization)or $6,000 if they suffer a minor injury (resulting in lost time from work).The company estimates that each year 1 in every 2,000 policyholders will have a major injury and 1 in every 400 a minor injury.What is the standard deviation of the company's profit on this policy?
(Multiple Choice)
4.7/5  (24)
(24)
Showing 41 - 60 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)