Exam 15: Random Variables
Exam 1: Data30 Questions
Exam 2: Displaying and Describing Categorical Data65 Questions
Exam 3: Displaying and Summarizing Quantitative Data93 Questions
Exam 4: Understanding and Comparing Distributions102 Questions
Exam 5: The Standard Deviation As a Ruler and the Normal Model131 Questions
Exam 6: Scatterplots, association, and Correlation74 Questions
Exam 7: Linear Regression57 Questions
Exam 8: Regression Wisdom32 Questions
Exam 9: Re-Expressing Data: Get It Straight51 Questions
Exam 10: Understanding Randomness26 Questions
Exam 11: Sample Surveys50 Questions
Exam 12: Experiments and Observational Surveys87 Questions
Exam 13: From Randomness to Probability64 Questions
Exam 14: Probability Rules90 Questions
Exam 15: Random Variables112 Questions
Exam 16: Probability Models114 Questions
Exam 17: Sampling Distribution Models45 Questions
Exam 18: Confidence Intervals for Proportions56 Questions
Exam 19: Testing Hypotheses About Proportions50 Questions
Exam 20: More About Tests69 Questions
Exam 21: Comparing Two Proportions52 Questions
Exam 22: Inferences About Means106 Questions
Exam 23: Comparing Means43 Questions
Exam 24: Paired Samples and Blocks33 Questions
Exam 25: Comparing Counts78 Questions
Exam 26: Inferences for Regression51 Questions
Exam 27: Analysis of Variance39 Questions
Exam 28: Multifactor Analysis of Variance22 Questions
Exam 29: Multiple Regression22 Questions
Exam 30: Multiple Regression Wisdom21 Questions
Exam 31: Rank-Based Nonparametric Tests29 Questions
Exam 32: The Bootstrap31 Questions
Select questions type
You roll a pair of fair dice.If you get a sum greater than 10 you win $50.If you get a double you win $40.If you get a double and a sum greater than 10 you win $90.Otherwise you win nothing.
Create a probability model for the amount you win at this game.
(Multiple Choice)
4.8/5  (32)
(32)
In a box of 7 batteries,6 are dead.You choose two batteries at random from the box.Let the random variable X be the number of good batteries you get.Find the expected value of X.
(Multiple Choice)
4.8/5  (24)
(24)
Your school's soccer team plays two games against another soccer team .The probability that your team wins the first game is 0.4.If your team wins the first game,the probability that they also win the second game is 0.5.If your team loses the first game,the probability that they win the second game is 0.2.Let the random variable X be the number of games won by your team.Find the standard deviation of X.
(Multiple Choice)
4.8/5  (36)
(36)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable X + Y.Round to two decimal places if necessary. 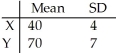
(Multiple Choice)
4.8/5  (30)
(30)
The amount of money that Maria earns in a week is a random variable with a mean of $970 and a standard deviation of $25.The amount of money that Elena earns in a week is a random variable with a mean of $860 and a standard deviation of $10.How much more do you expect Maria to earn in a week than Elena? What is the standard deviation of this difference? Assume that Maria's earnings are independent of Elena's earnings.
(Multiple Choice)
4.9/5  (34)
(34)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable 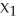 +
+ 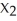 .
. 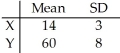
(Multiple Choice)
4.9/5  (36)
(36)
In the 4 × 100 relay event,each of four runners runs 100 metres.A university team is preparing for a competition.The means and standard deviations of the times (in seconds)of their four runners are as shown in the table: 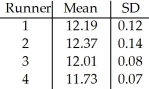 What are the mean and standard deviation of the relay team's total time in this event? Assume that the runners' performances are independent.
What are the mean and standard deviation of the relay team's total time in this event? Assume that the runners' performances are independent.
(Multiple Choice)
4.8/5  (35)
(35)
A teacher grading statistics homeworks finds that none of the students has made more than three errors.14% have made three errors,25% have made two errors,and 39% have made one error.Find the standard deviation of the number of errors in students' statistics homeworks.
(Multiple Choice)
4.8/5  (30)
(30)
At a furniture factory,tables must be assembled,finished,and packaged before they can be shipped to stores.Based on past experience,the manager finds that the means and standard deviations (in minutes)of the times for each phase are as shown in the table: 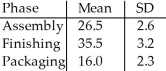 Find the probability that a table can be prepared for shipping in less than 67.61 minutes.
Assume that the times for each phase are independent and that the times for each phase follow a Normal model.
Find the probability that a table can be prepared for shipping in less than 67.61 minutes.
Assume that the times for each phase are independent and that the times for each phase follow a Normal model.
(Multiple Choice)
4.9/5  (37)
(37)
A couple plans to have children until they get a boy,but they agree that they will not have more than four children even if all are girls.
Find the standard deviation of the number of children the couple have.Assume that boys and girls are equally likely.Round your answer to three decimal places.
(Multiple Choice)
4.7/5  (33)
(33)
A company bids on two contracts.It anticipates a profit of $70,000 if it gets the larger contract and a profit of $30,000 if it gets the smaller contract.It estimates that there's a 10% chance of winning the larger contract and a 60% chance of winning the smaller contract.Find the standard deviation of the company's profit.Assume that the contracts will be awarded independently.
(Multiple Choice)
4.9/5  (40)
(40)
Suppose you pay $2.00 to roll a fair die with the understanding that you will get back $4.00 for rolling a 6 or a 3,nothing otherwise.What is the expected amount you win?
(Multiple Choice)
4.9/5  (40)
(40)
Showing 101 - 112 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)