Exam 15: Random Variables
Exam 1: Data30 Questions
Exam 2: Displaying and Describing Categorical Data65 Questions
Exam 3: Displaying and Summarizing Quantitative Data93 Questions
Exam 4: Understanding and Comparing Distributions102 Questions
Exam 5: The Standard Deviation As a Ruler and the Normal Model131 Questions
Exam 6: Scatterplots, association, and Correlation74 Questions
Exam 7: Linear Regression57 Questions
Exam 8: Regression Wisdom32 Questions
Exam 9: Re-Expressing Data: Get It Straight51 Questions
Exam 10: Understanding Randomness26 Questions
Exam 11: Sample Surveys50 Questions
Exam 12: Experiments and Observational Surveys87 Questions
Exam 13: From Randomness to Probability64 Questions
Exam 14: Probability Rules90 Questions
Exam 15: Random Variables112 Questions
Exam 16: Probability Models114 Questions
Exam 17: Sampling Distribution Models45 Questions
Exam 18: Confidence Intervals for Proportions56 Questions
Exam 19: Testing Hypotheses About Proportions50 Questions
Exam 20: More About Tests69 Questions
Exam 21: Comparing Two Proportions52 Questions
Exam 22: Inferences About Means106 Questions
Exam 23: Comparing Means43 Questions
Exam 24: Paired Samples and Blocks33 Questions
Exam 25: Comparing Counts78 Questions
Exam 26: Inferences for Regression51 Questions
Exam 27: Analysis of Variance39 Questions
Exam 28: Multifactor Analysis of Variance22 Questions
Exam 29: Multiple Regression22 Questions
Exam 30: Multiple Regression Wisdom21 Questions
Exam 31: Rank-Based Nonparametric Tests29 Questions
Exam 32: The Bootstrap31 Questions
Select questions type
Your school's soccer team plays two games against another soccer team .The probability that your team wins the first game is 0.4.If your team wins the first game,the probability that they also win the second game is 0.4.If your team loses the first game,the probability that they win the second game is 0.3.Let the random variable X be the number of games won by your team.Find the expected value of X.
(Multiple Choice)
4.9/5  (31)
(31)
You have arranged to go camping for two days in March.You believe that the probability that it will rain on the first day is 0.4.If it rains on the first day,the probability that it also rains on the second day is 0.5.If it doesn't rain on the first day,the probability that it rains on the second day is 0.3.Let the random variable X be the number of rainy days during your camping trip.Find the standard deviation of X.
(Multiple Choice)
4.7/5  (37)
(37)
The amount of money that Jon can save after working for a summer is a random variable S with a mean of  And a standard deviation of
And a standard deviation of 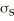 .After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of
.After saving this money Jon plans to go on a trip to India.He will change his money into Rupees at an exchange rate of 43 Rupees to one Dollar.This money he will bring to India.When he arrives in India he will buy a used motorbike.The price in India of a motorbike of the type he wants is a random variable B with a mean of 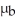 Rupees and a standard deviation of
Rupees and a standard deviation of 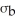 Rupees .
The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P which can be expressed in terms of S and B as P = 43S - B.
Find expressions for the mean and variance of the random variable P.Assume that Jon's savings and the price of the bike are independent.
Rupees .
The amount of money Jon will have left (in Rupees)after changing his savings into Rupees and buying a motorbike in India is a random variable P which can be expressed in terms of S and B as P = 43S - B.
Find expressions for the mean and variance of the random variable P.Assume that Jon's savings and the price of the bike are independent.
(Multiple Choice)
4.8/5  (34)
(34)
The probability model below describes the number of thunderstorms that a certain town may experience during the month of August. 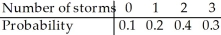 What is the standard deviation of the number of storms in August?
What is the standard deviation of the number of storms in August?
(Multiple Choice)
4.8/5  (40)
(40)
An insurance company estimates that it should make an annual profit of $140 on each homeowner's policy written,with a standard deviation of $5,500.If it writes 10,000 of these policies,what are the mean and standard deviation of the annual profit? Assume that policies are independent of each other.
(Multiple Choice)
4.7/5  (33)
(33)
The amount of time it takes to serve each customer in a bank is a random variable,X,with a mean of μ minutes and a standard deviation of σ minutes.When you arrive at the bank there are three customers in front of you.If the times for the three customers are independent of one another,which of the following shows the correct method for calculating the variance of your wait time?
(Multiple Choice)
4.7/5  (36)
(36)
At a furniture factory,tables must be assembled,finished,and packaged before they can be shipped to stores.Based on past experience,the manager finds that the means and standard deviations (in minutes)of the times for each phase are as shown in the table: 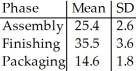 What are the mean and standard deviation of the total time to prepare a table for shipping? Assume that the times for each phase are independent.
What are the mean and standard deviation of the total time to prepare a table for shipping? Assume that the times for each phase are independent.
(Multiple Choice)
4.9/5  (31)
(31)
You pick a card from a deck.If you get a club,you win $80.If not,you get to draw again (after replacing the first card).If you get a club the second time,you win $30.Otherwise you win nothing.
Create a probability model for the amount you win at this game.
(Multiple Choice)
4.7/5  (46)
(46)
Janet is planning to rent a booth at a festival for a day to sell clothes that she has made.She sells jackets for $80 and skirts for $50.Her past experiences suggests that sales of jackets will have a mean of 6.5 with a standard deviation of  ,and sales of skirts will have a mean of 12.6 with a standard deviation of
,and sales of skirts will have a mean of 12.6 with a standard deviation of 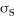 .The cost of renting the booth for the day is $180.Let the random variable J represent the number of jackets that Janet sells and the random variable S represent the number of skirts that Janet sells.Then Janet's net income,I,is given by the expression:
I = 80J + 50S - 180
Find an expression for the standard deviation of Janet's net income.Assume that sales are independent of each other.
.The cost of renting the booth for the day is $180.Let the random variable J represent the number of jackets that Janet sells and the random variable S represent the number of skirts that Janet sells.Then Janet's net income,I,is given by the expression:
I = 80J + 50S - 180
Find an expression for the standard deviation of Janet's net income.Assume that sales are independent of each other.
(Multiple Choice)
5.0/5  (39)
(39)
The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate Office.Its probability distribution is as follows.Find the standard deviation of the number of houses sold. 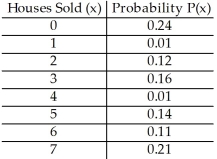
(Multiple Choice)
5.0/5  (35)
(35)
Janet is planning to rent a booth at a festival for a day to sell clothes that she has made.She sells jackets for $80 and skirts for $50.Her past experiences suggests that sales of jackets will have a mean of 6.5 with a standard deviation of 1.4,and sales of skirts will have a mean of 12.6 with a standard deviation of 2.7.The cost of renting the booth for the day is $180.Let the random variable J represent the number of jackets that Janet sells and the random variable S represent the number of skirts that Janet sells.Express Janet's net income,I,in terms of J and S.
(Multiple Choice)
4.8/5  (34)
(34)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable Y - 19.Round to two decimal places if necessary. 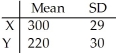
(Multiple Choice)
4.8/5  (34)
(34)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable X - Y.Round to two decimal places if necessary. 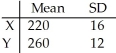
(Multiple Choice)
4.8/5  (23)
(23)
In the 4 × 100 relay event,each of four runners runs 100 metres.A college team is preparing for a competition.The means and standard deviations of the times (in seconds)of their four runners are shown in the table: 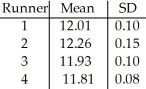 Find the probability that in the competition they will beat their previous best time of 47.501 sec.Assume that the runners' performances are independent and that each runner's time follows a Normal model.
Find the probability that in the competition they will beat their previous best time of 47.501 sec.Assume that the runners' performances are independent and that each runner's time follows a Normal model.
(Multiple Choice)
4.8/5  (42)
(42)
A carnival game offers a $80 cash prize for anyone who can break a balloon by throwing a dart at it.It costs $5 to play and you're willing to spend up to $20 trying to win.You estimate that you have a 8% chance of hitting the balloon on any throw.Find the standard deviation of the number of darts you throw.Assume that throws are independent of each other.
(Multiple Choice)
4.8/5  (35)
(35)
Given independent random variables with means and standard deviations as shown,find the mean and standard deviation of the variable 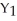 +
+ 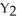 .
. 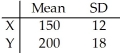
(Multiple Choice)
4.9/5  (27)
(27)
The amount of time it takes to serve each customer in a bank is a random variable with a mean of 3.7 minutes and a standard deviation of 2.1 minutes.When you arrive at the bank there are three customers in front of you.The mean of your wait time is 3 × 3.7 = 11.1 minutes.The standard deviation of your wait time is  ≈ 3.64 minutes.What assumptions (if any)underlie the calculation of the mean? of the standard deviation?
≈ 3.64 minutes.What assumptions (if any)underlie the calculation of the mean? of the standard deviation?
(Multiple Choice)
4.7/5  (34)
(34)
Suppose that in one town adult men have a mean weight of 77 kg with a standard deviation of 7 kg.Adult women have a mean weight of 63 kg with a standard deviation of 5 kg.10 year old children have a mean weight of 41 kg with a standard deviation of 3 kg.Suppose that a man,a woman,and a 10-year old child get into an elevator.What are the mean and standard deviation of their total weight?
(Multiple Choice)
4.7/5  (42)
(42)
A contractor is considering a sale that promises a profit of $24,000 with a probability of 0.7 or a loss (due to bad weather,strikes,and such)of $9,000 with a probability of 0.3.What is the expected profit?
(Multiple Choice)
4.8/5  (38)
(38)
Showing 21 - 40 of 112
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)