Exam 3: Differentiation Rules
Exam 1: Functions and Models118 Questions
Exam 2: Limits and Derivatives127 Questions
Exam 3: Differentiation Rules248 Questions
Exam 4: Applications of Differentiation273 Questions
Exam 5: Integrals239 Questions
Exam 6: Applications of Integration189 Questions
Exam 7: Differential Equations154 Questions
Exam 8: Infinite Sequences and Series341 Questions
Exam 9: Vectors and the Geometry of Space269 Questions
Exam 10: Vector Functions111 Questions
Exam 11: Partial Derivatives294 Questions
Exam 12: Multiple Integrals270 Questions
Exam 13: Vector Calculus240 Questions
Select questions type
A particle moves along a straight line with equation of motion . Find the value of t at which the particle reverses its direction.
(Multiple Choice)
4.8/5  (37)
(37)
f and g are functions whose graphs are shown below. Let and Find each derivative, if it exists. If it does not exist, explain. 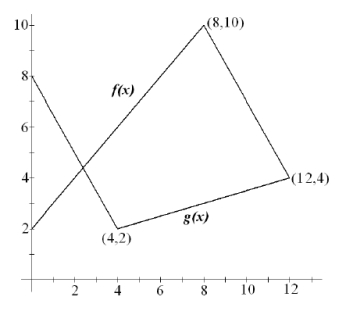 (a) (b) (c) (d) (e) (f) (g) (h) (i)
(a) (b) (c) (d) (e) (f) (g) (h) (i)
(Essay)
4.9/5  (40)
(40)
Find the y-intercept of the tangent line to the curve at the point (1, 2).
(Multiple Choice)
4.7/5  (45)
(45)
Find an equation of the tangent line to the curve at the point (1, 8).
(Essay)
4.8/5  (37)
(37)
A stone is thrown into a pond, creating a circular wave whose radius increases at the rate of 1 foot per second. In square feet per second, how fast is the area of the circular ripple increasing 3 seconds after the stone hits the water?
(Multiple Choice)
4.8/5  (43)
(43)
The position function for a particle is , where s is measured in feet and t is measured in seconds.(a) Find the velocity at t = 2.(b) When does the velocity equal zero?
(Short Answer)
4.8/5  (34)
(34)
The angular displacement of a simple pendulum is given by where is the angular amplitude, the angular frequency and a phase constant depending on initial conditions. If we are given that = 10 and
, find the angular velocity when .
(Essay)
4.9/5  (38)
(38)
Suppose that is a differentiable function. Find for each of the following, in terms of and .(a) (b) (c) (d)
(Essay)
4.9/5  (31)
(31)
Let be the amount of salt (in kg) in a tank after time t minutes. Find:
(a) How much salt is in the tank after 1 hour?
(b) Find the rate of change of salt after 1 hour?
(Essay)
4.7/5  (34)
(34)
Find the y-intercept of the tangent line to the curve at the point ( , 0).
(Essay)
4.8/5  (43)
(43)
Showing 141 - 160 of 248
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)