Exam 12: Parametric Equations and Polar Coordinates
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Graph the set of points whose polar coordinates satisfy the given equation or inequality.
-
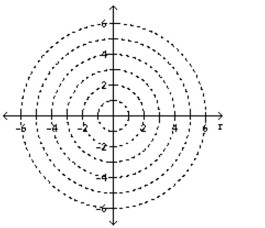
(Multiple Choice)
4.8/5  (36)
(36)
Assuming that the equations define x and y implicitly as differentiable functions x = f(t), y = g(t), find the slope of the curve x = f(t), y = g(t) at the given value of t.
-
(Multiple Choice)
5.0/5  (39)
(39)
Graph the pair of parametric equations with the aid of a graphing calculator.
-
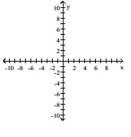
(Multiple Choice)
4.8/5  (34)
(34)
Find the slope of the polar curve at the indicated point.
-
(Multiple Choice)
4.9/5  (34)
(34)
Graph the set of points whose polar coordinates satisfy the given equation or inequality.
-
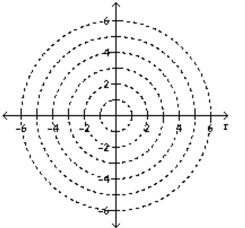
(Multiple Choice)
4.8/5  (31)
(31)
Determine if the given polar coordinates represent the same point.
-
(True/False)
4.9/5  (27)
(27)
Solve the problem.
-Find the point on the curve , closest to the point . (Hint: Minimize the square of the distance as a function of .)
(Multiple Choice)
4.9/5  (42)
(42)
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.
-Vertices at (2, 0) and (-2, 0); foci at (4, 0) and (-4, 0)
(Multiple Choice)
4.8/5  (36)
(36)
Find the coordinates of the centroid of the curve.
-Find the coordinates of the centroid of the curve .
(Multiple Choice)
4.8/5  (37)
(37)
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.
-Foci at ; asymptotes:
(Multiple Choice)
4.8/5  (47)
(47)
Showing 21 - 40 of 396
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)