Exam 12: Parametric Equations and Polar Coordinates
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Graph the parabola or ellipse. Include the directrix that corresponds to the focus at the origin.
-
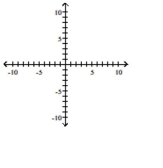
(Multiple Choice)
4.7/5  (39)
(39)
Find an equation for the line tangent to the curve at the point defined by the given value of t.
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the area of the specified region.
-Inside the smaller loop of the limacon
(Multiple Choice)
4.7/5  (41)
(41)
Solve the problem.
-The parabola is shifted up 7 units and left 7 units. Find an equation for the new parabola and find the new vertex.
(Multiple Choice)
4.9/5  (37)
(37)
Graph the set of points whose polar coordinates satisfy the given equation or inequality.
-
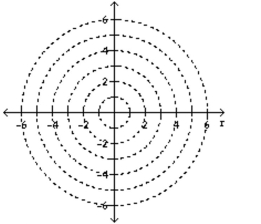
(Multiple Choice)
4.8/5  (32)
(32)
The eccentricity is given of a conic section with one focus at the origin, along with the directrix corresponding to that focus. Find a polar equation for the conic section.
-e = 2, x = -8
(Multiple Choice)
4.7/5  (34)
(34)
Provide an appropriate response.
-Assuming is continuous for and , what can be said about the relative areas betweel the origin and the polar curves and
=(\theta),\alpha\leq\theta\leq\beta =2(\theta),\alpha\leq\theta\leq\beta?
Give reasons for your answer.
(Essay)
5.0/5  (33)
(33)
Solve the problem.
-The hyperbola is shifted horizontally and vertically to obtain the hyperbola . Graph the new hyperbola.

(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-The ellipse is shifted horizontally and vertically to obtain the ellipse Graph the new ellipse.
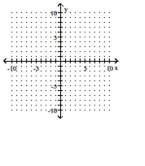
(Multiple Choice)
4.8/5  (30)
(30)
If the equation represents a hyperbola, find the center, foci, and asymptotes. If the equation represents an ellipse, find the center, vertices, and foci. If the equation represents a circle, find the center and radius. If the equation represents a parabola, find the focus and directrix.
-
(Multiple Choice)
4.9/5  (43)
(43)
Graph the pair of parametric equations with the aid of a graphing calculator.
-
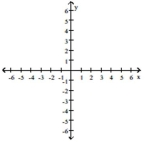
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-Find the volume generated by revolving about the -axis the area bounded by the curves
(Multiple Choice)
5.0/5  (35)
(35)
Showing 141 - 160 of 396
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)