Exam 12: Parametric Equations and Polar Coordinates
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Solve the problem.
-The parabola is shifted 7 units down and 2 units to the right. Find the focus and directrix of the new parabola.
(Multiple Choice)
4.9/5  (34)
(34)
Find the area of the specified region.
-Inside the cardioid
(Multiple Choice)
4.8/5  (45)
(45)
Find a Cartesian equation for the line whose polar equation is given.
-
(Multiple Choice)
4.9/5  (35)
(35)
The eccentricity is given of a conic section with one focus at the origin, along with the directrix corresponding to that focus. Find a polar equation for the conic section.
-
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-Find the foci and asymptotes of the following hyperbola:
(Multiple Choice)
4.7/5  (34)
(34)
Find the standard-form equation of the hyperbola centered at the origin which satisfies the given conditions.
-Vertices at (0, 6) and (0, -6); foci at (0, 9) and (0, -9)
(Multiple Choice)
4.8/5  (40)
(40)
Sketch the region which is defined by the given conditions.
-
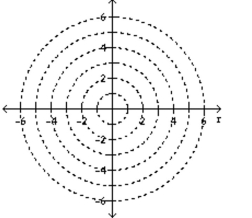
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Find the volume of the solid generated by revolving the region enclosed by the ellipse about the -axis.
(Multiple Choice)
4.8/5  (48)
(48)
Sketch the region which is defined by the given conditions.
-
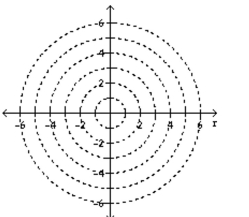
(Multiple Choice)
4.7/5  (43)
(43)
Parametric equations and and a parameter interval for the motion of a particle in the xy-plane are given. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph
traced by the particle and the direction of motion.
-
(Multiple Choice)
4.8/5  (40)
(40)
Find the standard-form equation for a hyperbola which satisfies the given conditions.
-A hyperbola centered at the origin having vertex at (0, -8) and eccentricity equal to 2
(Multiple Choice)
4.9/5  (36)
(36)
Find a Cartesian equation for the line whose polar equation is given.
-
(Multiple Choice)
4.8/5  (34)
(34)
Provide an appropriate response.
-Find the error in the following "proof" that the area inside the lemniscate is 0 and then find the correct area.
(Essay)
4.8/5  (31)
(31)
Showing 341 - 360 of 396
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)