Exam 12: Parametric Equations and Polar Coordinates
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
Find the standard-form equation for an ellipse which satisfies the given conditions.
-An ellipse centered at the origin having vertex at and eccentricity equal to
(Multiple Choice)
4.7/5  (27)
(27)
Solve the problem.
-The hyperbola is shifted horizontally and vertically to obtain the hyperbola .
Graph the new hyperbola.
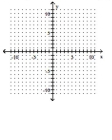
(Multiple Choice)
4.8/5  (35)
(35)
Replace the polar equation with an equivalent Cartesian equation.
-
(Multiple Choice)
5.0/5  (38)
(38)
Parametric equations and and a parameter interval for the motion of a particle in the xy-plane are given. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph
traced by the particle and the direction of motion.
-
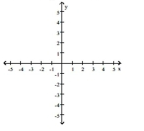
(Multiple Choice)
4.8/5  (39)
(39)
Find the standard-form equation of the ellipse centered at the origin and satisfying the given conditions.
-An ellipse with vertices and foci at .
(Multiple Choice)
4.8/5  (37)
(37)
Determine if the given polar coordinates represent the same point.
-
(True/False)
4.9/5  (25)
(25)
Find the slope of the polar curve at the indicated point.
-
(Multiple Choice)
4.8/5  (41)
(41)
The polar equation of a circle is given. Give polar coordinates for the center of the circle and identify its radius.
-
(Multiple Choice)
4.9/5  (32)
(32)
Replace the Cartesian equation with an equivalent polar equation.
-
(Multiple Choice)
4.8/5  (41)
(41)
Showing 181 - 200 of 396
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)