Exam 3: Limits and Continuity
Exam 2: Functions413 Questions
Exam 3: Limits and Continuity327 Questions
Exam 4: Derivatives560 Questions
Exam 5: Applications of Derivatives412 Questions
Exam 6: Integrals292 Questions
Exam 7: Applications of Definite Integrals258 Questions
Exam 8: Integrals and Transcendental Functions176 Questions
Exam 9: Techniques of Integration460 Questions
Exam 10: First-Order Differential Equations90 Questions
Exam 11: Infinite Sequences and Series473 Questions
Exam 12: Parametric Equations and Polar Coordinates396 Questions
Exam 13: Vectors and the Geometry of Space229 Questions
Exam 14: Vector-Valued Functions and Motion in Space142 Questions
Exam 15: Partial Derivatives409 Questions
Exam 16: Multiple Integrals435 Questions
Exam 17: Integrals and Vector Fields277 Questions
Select questions type
For the function f whose graph is given, determine the limit.
-
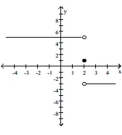
(Multiple Choice)
4.9/5  (43)
(43)
A function , a point , the limit of as approaches , and a positive number is given. Find a number such that for all .
- , and
(Multiple Choice)
4.8/5  (42)
(42)
Given the interval on the -axis with the point inside, find the greatest value for such that for all ,
-
(Multiple Choice)
4.8/5  (34)
(34)
Use the table of values of f to estimate the limit.
-Let , find
x -0.1 -0.01 -0.001 0.001 0.01 0.1 () 2.99955002 2.99955002
(Multiple Choice)
5.0/5  (41)
(41)
A function , a point , the limit of as approaches , and a positive number is given. Find a number such that for all .
-
(Multiple Choice)
4.8/5  (35)
(35)
Use a CAS to plot the function near the point x0 being approached. From your plot guess the value of the limit.
-
(Multiple Choice)
4.9/5  (31)
(31)
A function , a point , the limit of as approaches , and a positive number is given. Find a number such that for all .
- , and
(Multiple Choice)
4.9/5  (36)
(36)
Graph the rational function. Include the graphs and equations of the asymptotes.
-
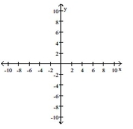
(Multiple Choice)
4.8/5  (37)
(37)
Because of their connection with secant lines, tangents, and instantaneous rates, limits of the form occur frequently in calculus. Evaluate this limit for the given value of and function .
-
(Multiple Choice)
4.8/5  (42)
(42)
Provide an appropriate response.
-Given , find an interval , such that if lies in , then . What limit is being verified and what is its value?
(Multiple Choice)
4.9/5  (31)
(31)
Showing 181 - 200 of 327
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)